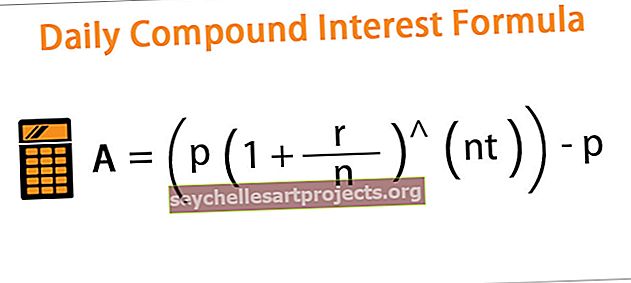seychellesartprojects.org

Regressiooni arvutamise valem

Regressioonivalemit kasutatakse sõltuva ja sõltumatu muutuja vahelise seose hindamiseks ja selle välja selgitamiseks, kuidas see mõjutab sõltuvat muutujat sõltumatu muutuja muutumisele ja on võrrandiga Y võrdne aX pluss b, kus Y on sõltuv muutuja, a on kalle regressioonivõrrandi korral on x sõltumatu muutuja ja b on konstant.

Regressioonanalüüsis kasutati laialdaselt statistilisi meetodeid ühe või mitme sõltumatu muutuja ja sõltuvate muutujate vaheliste seoste hindamiseks. Regressioon on võimas tööriist, kuna seda kasutatakse kahe või enama muutuja vahelise suhte tugevuse hindamiseks ja seejärel kasutatakse seda nende muutujate vahelise suhte modelleerimiseks tulevikus.

Y = a + bX + ∈

Kus:

• Y - on sõltuv muutuja
• X - on sõltumatu (selgitav) muutuja
• a - on pealtkuulamine
• b - on kalle
• ∈ - ja on jääk (viga)

Punkti "a" ja kalle "b" valemi saab arvutada allpool.

a = (Σy) (Σx2) - (Σx) (Σxy) / n (Σx2) - (Σx) 2 b = n  (Σxy) - (Σx) (Σy)  / n ( Σx2) - (Σx ) 2

Selgitus

Varem mainitud regressioonanalüüsi kasutatakse peamiselt andmetele sobivate võrrandite leidmiseks. Lineaaranalüüs on üks regressioonanalüüsi tüüp. Joone võrrand on y = a + bX. Y on sõltuv muutuja valemis, mida püütakse ennustada, milline on tulevane väärtus, kui X sõltumatu muutuja muutub teatud väärtuse võrra. Valemis “a” on lõikepunkt, mis on see väärtus, mis jääb fikseerituks sõltumata muutuja sõltumatust muutujast ja mõiste “b” valemis on kalle, mis tähistab, kui palju muutuja on sõltumatu muutuja sõltuv muutuja.

Näited

Selle regressioonivalemi Exceli malli saate alla laadida siit - regressioonivalemi Exceli mall

Näide 1

Vaatleme kahte järgmist muutujat x ja y, peate regressiooni arvutama.

Lahendus:

Kasutades ülaltoodud valemit, saame Excelis lineaarse regressiooni arvutada järgmiselt.

Meil on kõik ülaltoodud tabeli väärtused n = 5.

Nüüd kõigepealt arvutage regressiooni lõikepunkt ja kalle.

Intercepti arvutamine on järgmine,

a = (628,33 * 88 017,46) - (519,89 * 106 206,14) / 5 * 88 017,46 - (519,89) 2

a = 0,52

Kallakuse arvutamine on järgmine,

b = (5 * 106 206,14) - (519,89 * 628,33) / (5 * 88 017,46) - (519,89) 2

b = 1,20

Regressiooni saamiseks sisestame nüüd regressioonivalemis olevad väärtused.

Seega regressioonijoon Y = 0,52 + 1,20 * X 

Näide 2

India riigipank kehtestas hiljuti uue hoiukonto intressimäära sidumise repo määraga ja India osariigi panga audiitor soovib läbi viia panga intressimuutustega seotud otsuste sõltumatu analüüsi, olenemata sellest, kas neid on muudetud alati Repo intressimääras on toimunud muudatusi. Allpool on toodud Repo intressimäära kokkuvõte ja panga hoiukonto intressimäär, mis valitses neil kuudel.

Riigipanga audiitor on pöördunud teie poole, et järgmisel koosolekul analüüsida ja samal teemal ettekanne pidada. Kasutage regressioonivalemit ja tehke kindlaks, kas panga intressimäär muutus tagasiostumäära muutmise ajal?

Lahendus:

Eespool käsitletud valemi abil saame arvutada lineaarse regressiooni excelis. Repo-intressimäära käsitlemine sõltumatu muutujana, st X ja Panga intressimäära kui sõltuva muutujana Y

Meil on kõik ülaltoodud tabeli väärtused n = 6.

Nüüd kõigepealt arvutage regressiooni lõikepunkt ja kalle.

Intercepti arvutamine on järgmine,

a = (24,17 * 237,69) - (37,75 * 152,06) / 6 * 237,69 - (37,75) 2

a = 4,28

Kallakuse arvutamine on järgmine,

b = (6 * 152,06) - (37,75 * 24,17) / 6 * 237,69 - (37,75) 2

b = -0,04

Joonise saamiseks sisestame nüüd valemis olevad väärtused.

Seega regressioonijoon Y = 4,28 - 0,04 * X

Analüüs: Näib, et India riigipank järgib reeglina oma säästumäära sidumist repo intressimääraga, kuna on olemas mõni kalle väärtus, mis annab märku seosest repo intressimäära ja panga säästukonto intressimäära vahel.

Näide # 3

ABC laboratoorium viib läbi pikkuse ja kaalu uuringuid ning soovis teada, kas on mingeid seoseid, nagu ka pikkuse kasvades kaalu suurenemine. Nad on kogunud igasse kategooriasse 1000 inimese valimi ja mõelnud selle rühma keskmise pikkuse.

Allpool on üksikasjad, mille nad on kogunud.

Te peate arvutama regressiooni ja jõudma järeldusele, et selline seos on olemas.

Lahendus:

Eespool käsitletud valemi abil saame arvutada lineaarse regressiooni excelis. Kõrguse käsitlemine sõltumatu muutujana, st X ja kaalu käsitlemine sõltuva muutujana Y-na.

Meil on kõik ülaltoodud tabeli väärtused n = 6

Nüüd kõigepealt arvutage regressiooni lõikepunkt ja kalle.

Intercepti arvutamine on järgmine,

a = (350 * 120 834) - (850 * 49 553) / 6 * 120 834 - (850) 2

a = 68,63

Kallakuse arvutamine on järgmine,

b = (6 * 49 553) - (850 * 350) / 6 * 120 834 - (850) 2

b = -0,07

Joonise saamiseks sisestame nüüd valemis olevad väärtused.

Seega on regressioonijoon Y = 68,63 - 0,07 * X

Analüüs: Tundub, et pikkuse ja kaalu vahel on märkimisväärselt vähem seos, kuna kalle on väga madal.

Regressioonivalemi asjakohasus ja kasutusalad

Kui korrelatsioonikordaja näitab, et andmed suudavad ennustada tulevasi tulemusi ja koos sellega näib, et sama andmekogumi hajuvusdiagramm moodustab lineaarse või sirge joone, saab ennustava tulemuse leidmiseks kasutada lihtsat lineaarset regressiooni väärtus või ennustav funktsioon. Regressioonanalüüsil on finantsvaldkonnas palju rakendusi, kuna seda kasutati CAPM-is, mis on kapitalivarade hinnakujundusmudel finantsmeetodiks. Seda saab kasutada ettevõtte tulude ja kulude prognoosimiseks.