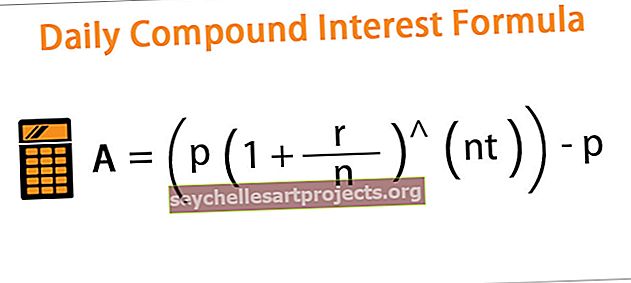seychellesartprojects.org

Mis on vahemiku valem?

Vahemiku valem viitab valemile, mida kasutatakse vahemiku maksimaalse ja minimaalse väärtuse erinevuse arvutamiseks ning valemi kohaselt lahutatakse minimaalne väärtus maksimaalsest väärtusest vahemiku määramiseks.

Vahemik = maksimaalne väärtus - minimaalne väärtus

Antud andmekogumist, mis võimaldab statistikutel ja matemaatikul andmekogumist paremini mõista, kui mitmekesine see on. Statistika dispersiooni arvutamiseks on kõige lihtsam lähenemisviis.

Selgitus

See on üsna lihtne ja hõlpsasti kasutatav, kuna valemis on märgitud selle maksimaalne väärtus miinimumväärtusest antud proovil. Seetõttu on maksimaalse väärtuse ja minimaalse väärtuse dispersioon vahemik ja isegi kui seda on lihtne kasutada ja mõista, on vaja seda õigesti tõlgendada.

Näiteks kui andmetes on piirjoon, mõjutaks see sama vahemikku ja tulemuse saamine tooks kaasa valeandmete esitamise. Võtke antud andmete 2, 4, 7, 7, 100 praktiline näide, siis oleks vahemik 100 - 2, mis on 98, kuid nagu on näha, et andmevahemik jääb alla 10, kuid arvestades ja tõlgendades, et andmed on 98 piires, valeandmete esitamiseks. Seetõttu tuleks vahemiku tõlgendamine läbi viia nõuetekohaselt.

Näited

Selle Range Formula Exceli malli saate alla laadida siit - Range Formula Exceli mall

Näide 1

Kaaluge järgmise andmekogumi 2,2,4,4, 4, 6,7,7,8, 8, 8, 9, 9, 9, 9, 9 järgimist. Te peate selle valimi vahemiku arvutama.

Lahendus:

• Maksimaalne väärtus = 9
• Minimaalne väärtus = 2

Vahemik = 9 - 2

Vahemik = 7

Näide 2

Hr Stark, teadlane, kes töötab kümme aastat ettevõttes Dream moon. Tema juhendaja hr Arora viib läbi katse inimeste tervisega ja on kogunud vähe meeste pikkusega valimiandmeid (162, 158, 189, 144, 151, 150, 151, 178, 155, 160). teada, kui palju andmeid on mitmekesine. Tema juhendaja hr Arora pöördus kogenud statistiku hr Starki poole, et kõrvaldada segadus valemi varieerumise osas. Hr Arora peab vastama oma juhendajale, peate arvutama, kui palju andmeid varieerub?

Lahendus:

Vahemik = maksimaalne väärtus - minimaalne väärtus

• Maksimaalne väärtus = 189
• Minimaalne väärtus = 144

Vahemik = 189 - 144

Vahemik = 45

Kogutud andmete või valimi variatsioon on 45.

Näide # 3

Hr Buffet, tuntud ja hinnatud investor kogu maailmas, kaalub nüüd USA turu aktsiaid ja analüüsib mõnda neist, kuhu ta soovib investeerida. Nimekirjas on USA suuremad sinise kiibiga ettevõtted. Allpool on toodud valitud nimekirja kantud aktsiad või väärtpaberid koos nende viimase aktsiaturu hinnaga, mis on tähistatud USA dollarites, kuhu ta kaalub investeerimist.

Peate arvutama vahemiku ja pakkuma välja loendi variatsiooni.

Lahendus:

Allpool on toodud andmed vahemiku arvutamiseks.

Kasutades ülaltoodud teavet, arvutatakse Exceli maksimaalne väärtus järgmiselt,

Maksimaalne väärtus = 204,66

Min-väärtuse arvutamine Excelis järgmiselt:

Minimaalne väärtus = 45,93

Seetõttu on vahemiku arvutamine järgmine,

Vahemik = 204,66 - 45,93

Vahemik saab olema -

Vahemik = 158,73

Range Formula kasutamine

Vahemik on omal moel väga lihtne ja väga lihtne mõista, kuidas antud andmekogumis või valimis olevad numbrid on hajutatud, sest nagu varem öeldud, on arvutust suhteliselt lihtne teha, kuna see on väga põhiline aritmeetiline toiming, mis lahutab maksimumväärtusest vaid miinimumi, kuid vahemikku on statistikas antud andmekogumi või antud valimi jaoks veel vähe rakendusi. Vahemik on kasulik ka teise levimismõõdu hindamiseks, mida nimetatakse dispersiooniks või standardhälbeks.

Varem mainitud vahemik võib anda teavet ainult põhiandmete kohta, st kus asub antud valimi või andmekogumi levik. Andes erinevuse või öeldes dispersiooni antud valimi või antud andmekogumi kõrgeima ja madalaima väärtuse vahel, annab see teabe või ligikaudse ülevaate oluliste äärmuslike vaatluste kohta, kui laialt levinud need on, kuid jällegi annab see pole ühtegi vihjet ega muud teavet muude andmepunktide kohta, kus need asuvad, mis on vahemiku võrrandi kasutamise peamine nõrkus.

Eespool käsitletud vahemik on kasulik leviku kujutamiseks antud proovis või antud andmekogumis ning seda kasutatakse ka tulemuste leviku võrdlemiseks sama antud valimi või samade andmekogumite vahel.