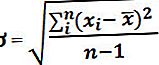Standardhälbe valemi näidis

Standardhälbe valemi näidis | Kuidas arvutada?

Standardproovi standardhälbe arvutamise valem

Valimi standardhälve viitab statistilisele mõõdikule, mida kasutatakse juhusliku suuruse valimi keskmisest lahknevuse mõõtmiseks ja selle arvutamiseks liidetakse iga muutuja keskmisest kõrvalekalde ruudud, seejärel jagatakse tulemus arv muutujaid, millest on lahutatud ja seejärel arvutatakse ruutjuur tulemuse excelis.

Matemaatiliselt on see esindatud järgmiselt:

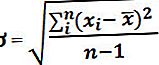
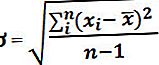
kus

x _i = juhuslik muutuja
X = valimi keskmine
n = valimi muutujate arv

Standardhälbe valimi arvutamine (samm-sammult)

1. samm: esiteks koguge juhuslikud muutujad suure hulga muutujate populatsioonist. Need muutujad moodustavad valimi. Muutujaid tähistatakse x _i-ga .
2. samm: Seejärel määrake valimis olevate muutujate arv ja seda tähistatakse n-ga.
3. samm: Seejärel määrake valimi keskmine, lisades kõik juhuslikud muutujad ja jagades tulemuse valimis olevate muutujate arvuga. Valimi keskmist tähistatakse x-ga.

4. samm: Järgmisena arvutage valimi iga muutuja ja valimi keskmise, st x _i - x vahe .
5. samm: Seejärel arvutage kõigi kõrvalekallete ruut, st (x _i - x) 2.
Samm 6: Järgmisena lisage kõik hälbed ruudust, st ie (x _i - x) 2.
7. samm: Järgmisena jagage kõigi ruutude kõrvalekallete liitmine valimis olevate muutujate arvuga miinus üks (n - 1).
8. samm: lõpuks arvutatakse standardhälbe valemi valem, arvutades ülalnimetatud tulemuse ruutjuure, nagu allpool näidatud.

Näited

Selle standardhälbe valemi Exceli malli näidise saate alla laadida siit - standardhälbe valemi Exceli malli näidis

Näide 1

Võtame näiteks 5 õpilase valimi, keda uuriti, et näha, mitu pliiatsit nad iga nädal kasutasid. Arvutage standardhälve valemi põhjal nende vastuste põhjal: 3, 2, 5, 6, 4

Arvestades

Valimi suurus (n) = 5

Allpool on esitatud andmed valimi standardhälbe arvutamiseks.

Keskmine proov

Proovi keskmise arvutamine

Valimi keskmine = (3 + 2 + 5 + 6 + 4) / 5

Valimi keskmine = 4

Iga muutuja hälvete ruudud saab arvutada järgmiselt:

(3 - 4) 2 = 1
(2 - 4) 2 = 4
(5–4) 2 = 1
(6 - 4) 2 = 4
(4 - 4) 2 = 0

Nüüd saab proovi standardhälbe arvutada ülaltoodud valemi abil järgmiselt:

ơ = √ {(1 + 4 + 1 + 4 + 0) / (5 - 1)}

Kõrvalekalle on -

ơ = 1,58

Seetõttu on valimi standardhälve 1,58.

Näide 2

Võtame näiteks New Yorgis asuva büroo, kus töötab umbes 5000 inimest ja töötava elanikkonna keskmise vanuse määramiseks on läbi viidud 10 inimese valimi uuring. Määrake valimi standardhälve 10 antud inimese vanuse põhjal: 23, 27, 33, 28, 21, 24, 36, 32, 29, 25

Arvestades

Valimi suurus (n) = 10

Kasutades ülaltoodud andmeid, arvutame kõigepealt valimi keskmise

Keskmine proov

Proovi keskmise arvutamine

= (23 + 27 + 33 + 28 + 21 + 24 + 36 + 32 + 29 + 25) / 10

Valimi keskmine = 27,8

Iga muutuja hälvete ruudud saab arvutada järgmiselt:

(23 - 27,8) 2 = 23,04
(27 - 27,8) 2 = 0,64
(33 - 27,8) 2 = 27,04
(28 - 27,8) 2 = 0,04
(21 - 27,8) 2 = 46,24
(24 - 27,8) 2 = 14,44
(36 - 27,8) 2 = 67,24
(32 - 27,8) 2 = 17,64
(29 - 27,8) 2 = 1,44
(25 - 27,8) 2 = 7,84

Hälve

Nüüd saab kõrvalekalde arvutada, kasutades ülaltoodud valemit,

ơ = √ {(23,04 + 0,64 + 27,04 + 0,04 + 46,24 +14,44 +67,24 + 17,64 + 1,44 + 7,84) / (10 - 1)}

Kõrvalekalle on -

ơ = 4,78

Üksikasjaliku arvutuse mõistmiseks võite viidata ülaltoodud Exceli lehele.

Asjakohasus ja kasutusalad

Standardhälbe valimi mõiste on statistiku seisukohast väga oluline, kuna tavaliselt võetakse andmete valim suurte muutujate kogumist (populatsioon), millest statistik eeldatavasti kogu populatsiooni tulemusi hindab või üldistab. Standardhälbe mõõt ei ole sellest erand ja seetõttu peab statistik koostatud valimi põhjal hinnangu andma populatsiooni standardhälbele ja just siis selline hälve mängu tuleb.

seychellesartprojects.org