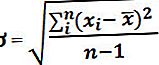seychellesartprojects.org

Normaalne jaotusvalem

Normaaljaotus on jaotus, mis on sümmeetriline, st positiivsed väärtused ja negatiivsed jaotuse väärtused saab jagada võrdseks pooleks ja seetõttu on keskmine, mediaan ja režiim võrdsed. Sellel on kaks saba, üks on tuntud kui parem saba ja teine ​​on vasak saba.

Arvutamise valemit saab esitada järgmiselt:

X ~ N (µ, α)

Kus

• N = vaatluste arv
• μ = vaatluste keskmine
• α = standardhälve

Enamasti ei paljasta vaatlusi toorel kujul. Seega on tähelepanekute standardimine selle võrdlemiseks väga oluline. Seda tehakse z-skoori valemi abil. Vaatluse jaoks on vaja arvutada Z-skoor.

Normaaljaotuse Z-skoori arvutamise võrrand on esitatud järgmiselt:

Z = (X-u) / a

Kus

• Z = vaatluste Z-skoor
• μ = vaatluste keskmine
• α = standardhälve

Selgitus

Jaotus on normaalne, kui see järgib kellakõverat. Seda tuntakse kellakõverana, kuna see võtab kella kuju. Normaalse kõvera üks olulisemaid omadusi on see, et see on sümmeetriline, mis tähendab, et jaotuse positiivsed ja negatiivsed väärtused saab jagada võrdseks pooleks. Teine muutuja olendi väga oluline omadus on see, et vaatlused jäävad 1 standardhälbe piiridesse keskmise 90% ajast. Vaatlused on kaks standardhälvet keskmisest 95% ajast ja see jääb kolme standardhälbe piiresse keskmisest 99% ajast.

Näited

Selle Normal Distribution Formula Exceli malli saate alla laadida siit - Normal Distribution Formula Exceli mall

Näide 1

Õpilaste klassi kaalu keskmine on 65 kg ja kaalu standard on 5 kg. Kui eeldame, et tootluse jaotus on normaalne, tõlgendagem siis klassi õpilaste kaalu järgi .

Kui jaotus on normaalne, siis 68% sellest jääb 1 standardhälbe, 95% 2 standardhälbe ja 99% 3 standardhälbe piiridesse.

Arvestades

• Kaalu keskmine tootlus on 65 kg
• Standardhälve on 3,5 kg

Seega on jaotuse väärtus 68% ajast allpool toodud vahemikus,

• Ülemine vahemik = 65 + 3,5 = 68,5
• Alumine vahemik = 65-3,5 = 61,5
• Iga saba (68% / 2) = 34%

Näide 2

Jätkame sama näitega. Õpilaste klassi kaalu keskmine on 65kg ja kaalu norm 3,5 kg. Kui eeldame, et tootluse jaotus on normaalne, siis tõlgendagem seda klassi õpilaste kaalu järgi.

Arvestades

• Kaalu keskmine tootlus on 65 kg
• Standardhälve on 3,5 kg

Seega on jaotuse väärtus 95% ajast allpool toodud vahemikus,

• Ülemine vahemik = 65 + (3,5 * 2) = 72
• Alumine vahemik = 65- (3,5 * 2) = 58
• Iga saba (95% / 2) = 47,5%

Näide # 3

Jätkame sama näitega. Õpilaste klassi kaalu keskmine on 65kg ja kaalu norm 3,5 kg. Kui eeldame, et tootluse jaotus on normaalne, siis tõlgendagem seda klassi õpilaste kaalu järgi.

Arvestades

• Kaalu keskmine tootlus on 65 kg
• Standardhälve on 3,5 kg

Seega on jaotuse väärtus 99% ajast allpool toodud vahemikus,

• Ülemine vahemik = 65+ (3,5 * 3) = 75,5
• Alumine vahemik = 65- (3,5 * 3) = 54,5
• Iga saba (99% / 2) = 49,5%

Asjakohasus ja kasutamine

Normaaljaotus on väga oluline statistiline mõiste, kuna enamik finantsmaailma juhuslikke muutujaid järgib sellist kõverat. Sellel on oluline osa portfellide koostamisel. Lisaks rahandusele leitakse, et sellist jaotust järgivad paljud reaalse elu parameetrid. Nagu näiteks siis, kui püüame leida õpilaste pikkust klassis või õpilaste kaalu klassis, jaotatakse vaatlused normaalselt. Samamoodi järgivad sama jaotust ka eksami hinded. Eksamite hinded aitab normaliseerida, kui enamik õpilastest hindasid alla sooritatavate hindete, seades piiri öelda, et ainult need, kes ebaõnnestusid, said alla kahe standardhälbe.