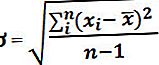seychellesartprojects.org

Valem õpilase T-jaotuse arvutamiseks

T-jaotuse arvutamise valem (mida rahva seas tuntakse ka kui Tudengi T-jaotust) on näidatud kui Populatsiooni keskmise (teise valimi keskmine) lahutamine valimi keskmisest (esimese valimi keskmine), mis on [x-bar - μ], mis on jagatakse siis keskväärtuste standardhälbega, mis jagatakse esialgu ruutjuurega n, mis on selle valimi ühikute arv [s ÷ √ (n)].

T jaotus on omamoodi jaotus, mis näeb välja peaaegu nagu tavaline jaotuskõver või kellakõver, kuid natuke paksema ja lühema sabaga. Kui valimi suurus on väike, kasutatakse seda jaotust normaaljaotuse asemel.

Kus

• x̄ on valimi keskmine
• μ on populatsiooni keskmine
• s on standardhälve
• n on antud valimi suurus

T-jaotuse arvutamine

Õpilase t jaotuse arvutamine on üsna lihtne, kuid jah, väärtused on vajalikud. Näiteks on vaja populatsiooni keskmist, mis on universumi tähendus, mis pole midagi muud kui populatsiooni keskmine, samas kui populatsiooni autentsuse testimiseks on vaja valimi keskmist, kas populatsiooni põhjal väidetud väide on tõene ja kui see on võetud esindavad sama väidet. Niisiis lahutab t jaotuse valem siin valimi keskmise populatsiooni keskmisest ja jagab selle seejärel standardhälbega ning korrutab valemi suuruse ruutjuurega, et väärtust standardiseerida.

Kuid kuna t jaotuse arvutamiseks ei ole vahemikku, võib väärtus minna imelikuks ja me ei saa arvutada tõenäosust, kuna õpilase t jaotusel on väärtuse saavutamiseks piirangud ja seetõttu on see kasulik ainult väiksema valimi suuruse korral. Samuti tuleb tõenäosuse arvutamiseks pärast skoori jõudmist leida selle väärtus õpilase t jaotustabelist.

Näited

Selle T Distribution Exceli malli saate alla laadida siit - T Distribution Exceli mall

Näide 1

Mõelge järgmistele muutujatele:

• Elanike keskmine = 310
• Standardhälve = 50
• Valimi suurus = 16
• Valimi keskmine = 290

Arvutage t-jaotuse väärtus.

Lahendus:

T jaotuse arvutamiseks kasutage järgmisi andmeid.

Seega saab T-jaotuse arvutada järgmiselt

Siin on kõik väärtused antud, peame lihtsalt väärtused kaasama.

Saame kasutada t jaotuse valemit

T väärtus = (290 - 310) / (50 / √16)

T väärtus = -1,60

Näide 2

SRH ettevõte väidab, et selle töötajad teenivad analüütikute tasemel keskmiselt 500 dollarit tunnis. Valitakse analüütikute tasemel 30 töötajat ja nende keskmine töötasu tunnis oli 450 dollarit valimi kõrvalekaldega 30 dollarit ja eeldades, et nende väide vastab tõele, arvutage t -jaotuse väärtus, mida kasutatakse t tõenäosuse leidmiseks - levitamine.

Lahendus:

T jaotuse arvutamiseks kasutage järgmisi andmeid.

Seega saab T-jaotuse arvutada järgmiselt

Siin on kõik väärtused antud, peame lihtsalt väärtused kaasama.

Saame kasutada t jaotuse valemit

T väärtus (450–500) / (30 / √30)

T väärtus = -9,13

Seega on t-skoori väärtus -9,13

Näide # 3

Universaalse kolledži juhatus oli IQ taseme testi korraldanud 50 juhuslikult valitud professorile. Ja tulemus, mille nad leidsid sellest, oli keskmine IQ taseme skoor 120 koos variatsiooniga 121. Oletame, et t skoor on 2.407. Mis on selle testi populatsiooni keskmine, mis õigustaks t skoori väärtuseks 2.407?

Lahendus:

T jaotuse arvutamiseks kasutage järgmisi andmeid.

Siin antakse kõik väärtused koos t väärtusega, peame seekord t väärtuse asemel arvutama populatsiooni keskmise.

Jällegi kasutaksime olemasolevaid andmeid ja arvutaksime populatsiooni keskmised, sisestades allpool toodud valemis toodud väärtused.

Valimi keskmine on 120, populatsiooni keskmine pole teada, valimi standardhälve on dispersioonruutu ruutjuur, mis oleks 11 ja valimi suurus 50.

Seega saab populatsiooni keskmise (μ) arvutada järgmiselt

Saame kasutada t jaotuse valemit

Väärtus t = (120 - μ) / (11 / √50)

2.407 = (120 - μ) / (11 / √50)

-μ = -2,407 * (11 / √50) -120

Populatsiooni keskmine (μ) on -

μ = 116,26

Seega on elanikkonna keskmise väärtuseks 116,26

Asjakohasus ja kasutamine

T-jaotust (ja nendega seotud t-skoori väärtusi) kasutatakse hüpoteeside testimisel, kui on vaja teada saada, kas nullhüpotees tuleb tagasi lükata või aktsepteerida.

Ülaltoodud graafikul on keskseks piirkonnaks vastuvõtupiirkond ja sabapiirkonnaks tagasilükkamispiirkond. Selles graafikus, mis on 2-sabaline test, on sinine varjutatud tagasilükkamispiirkond. Saba piirkonna piirkonda saab kirjeldada kas t-skooride või z-skooride abil. Võtke näide: vasakpoolsel pildil on kujutatud ala sabades viie protsendi ulatuses (mis on mõlemal küljel 2,5%). Z-skoor peaks olema 1,96 (võttes väärtuse z-tabelist), mis tähistab seda 1,96 standardhälvet keskmisest või keskmisest. Nullhüpoteesi saab tagasi lükata, kui z-skoori väärtus on väiksem kui -1,96 või kui z-skoori väärtus on suurem kui 1,96.

Üldiselt kasutatakse seda jaotust varem kirjeldatud viisil, kui valimi suurus on väiksem (enamasti alla 30) või kui ei tea, mis on populatsiooni dispersioon või populatsiooni standardhälve. Praktilistel eesmärkidel (see on reaalses maailmas) oleks see enamasti alati nii. Kui esitatud valimi suurus on piisavalt suur, on 2 jaotust praktiliselt sarnased.