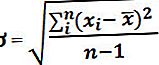seychellesartprojects.org

Mis on tootlus?

Kasumimäär on tootlus, mida investor oma investeeringult ootab, ja see arvutatakse põhimõtteliselt protsendina koos investeeringu keskmise tootluse (või kasumi) loenduriga ja sellega seotud investeeringu nimetajaga.

Tagasimäära valem

Valemi saab tuletada järgmiselt:

Kasumimäär = keskmine tootlus / alginvesteering

See on väga dünaamiline kontseptsioon investeeringutasuvuse mõistmiseks; seetõttu saab seda erinevatelt teedelt saadava tulu arvutamiseks veidi muuta ja kohandada.

• Keskmine tootlus: tootlus, mis mõõdetakse pärast kõigi hoiuperioodi kulude, sh haldustasude, makstud lisatasu (kui see on olemas), muude tegevuskulude jne sisestamist. Kõik tulud ja kulud peaksid olema seotud ainult kõnealuse varaga, muidu võib see erineda täpsed tulemused.
• Alginvesteering: algselt vara ostmiseks tehtud investeering 0. perioodil.

Näited

Selle vormingu Exceli tootluse tagasimaksumäära saate alla laadida siit - tootluse valemi Exceli mall

Näide 1

Annale kuulub tooteauto, ta investeeris veoki ostmisse 700 dollarit, mõned muud esialgsed administraatoriga seotud ja kindlustuskulud 1500 dollarit, et äri käima saada, ja nüüd on tal igapäevased kulutused 500 dollarit. Mõelgem hüpoteetiliselt, et tema igapäevane kasum on 550 dollarit (ideaalis põhineb see müügil). Kuue kuu lõpus võtab Anna oma kontod kokku ja arvutab oma tasuvuse määra. 

• Esialgne investeering kokku: 2200 dollarit
• Igapäevased kulud: 500 dollarit
• 6 kuu kogukulud: 3000 dollarit
• Iga päev naaseb: 550 dollarit
• 6 kuu kogutootlus: 3300 dollarit

Seega on tootluse määra arvutamiseks järgmised andmed:

Kasumimäär = ((kogu tootlus - kogukulud) / kogu alginvesteering) * 100

= (3 300–3 000 dollarit) / 2200 dollarit X 100

Seega on tasuvuse määr:

Näide 2

Joe on investeerinud võrdselt kahte väärtpaberisse A ja B. Ta soovib välja selgitada, milline väärtpaber lubab 2 aasta pärast suuremat tootlust. Samamoodi soovib ta otsustada, kas ta peaks hoidma teist väärtpaberit või likvideerima sellise positsiooni.

Uurime kõigilt väärtpaberitelt saadud tulud kõigepealt 1 aasta lõpus.

Liitintresside arvutatav tootlus on järgmine:

Allpool on tema investeeringuga seotud statistika:

Turvalisus A :

Investeering: 10 000 dollarit

Intressimäär: 5% makstakse igal aastal, arvestatuna

Tähtaeg: 10 aastat

A = PX [1 + R / n] ^ (nT)

kus:

• A = summa (või tootlus) pärast kindlat arvutusperioodi
• P = juhataja
• R = intressimäär
• n = intressimaksete sagedus
• T = arvutusperiood

Seega arvutatakse tagatise A (A1) tasuvuse määr järgmiselt -

A = PX [1 + R / n] ^ (nT)

Seetõttu naaske pärast 2 aastat turvalisuse A (A ₁ ) = 10 000 dollarit X [(1 + 0,05) ^ 2]

Niisiis, tagastuse A (A ₁ ) tagastamine 2 aasta pärast on järgmine:

Tagasitulek A (A1) 2 aasta pärast tagasi = 11 025 dollarit .

Turvalisus B :

Investeering: 10 000 dollarit

Intressimäär: 5% makstakse poolaastas, liidetud baasil

Tähtaeg: 10 aastat

Seetõttu on tagatise B (A ₂ ) tagastamise arvutamine 2 aasta pärast = 10 000 USD X [(1 + 0,05 / 2) ^ 4]

Niisiis, naaske 2 aasta pärast turvalisuse B (A2) eest = 11 038,13 dollarit

Analüüs:

Tehakse kindlaks, et kuigi tulud on sarnased, annab turva B siiski natuke tagasi. Teise positsiooni täielikku likvideerimist ei nõuta, kuna kahe tagastamise vahe on minimaalne, kuna A-turvalisuse hoidmine sellist Joe ei kahjusta.

Näide # 3

Joe soovib nüüd arvutada tootlust pärast 10. aastat ja tahab hinnata tema investeeringut.

Liitintressi valemi põhjal arvutatud tootluse põhjal saame arvutada 10 aasta jooksul järgmiselt:

Niisiis, väärtpaberi A (A1) tasuvusmäära arvutamine kümneks aastaks on järgmine -

A = PX [1 + R / n] ^ (nT)

Seetõttu on tagatise A (A ₁ ) 10 aasta tootluse arvutamine 10 000 dollarit X [(1+ 0,05) ^ 10]

Seega tagastatakse turvalisuse A (A ₁ ) kümneks aastaks kümneks aastaks:

Turvalisuse A (A ₁ ) 10-aastane tootlus =   16 288,95 dollarit.

Seetõttu naaske pärast 10 aastat turvalisuse B (A ₂ ) = 10 000 dollarit X [(1 + 0,05 / 2) ^ 20]

Turvalisuse B (A2) naasmine 10 aasta pärast =  16 386,16 dollarit

Asjakohasus ja kasutamine

• Iga investor on avatud riskidele ja tootlusele. Puiestee pakutavad tulud võivad olla või mitte olla tegelikud tulud teatud aja jooksul vara riskantsusest turgudel. Seetõttu on äärmiselt oluline mõista investeeringu tegelikku tootlust.
• See aitab otsustada kapitali eelarvestamisel. See aitab kindlaks teha, kas konkreetsesse projekti investeerimine on teatud aja jooksul kasulik, ja valida võimaluste vahel, võrreldes ja tuvastades parima ettevõtmise.
• See viitab turul valitsevatele suundumustele ja võib mõnikord viidata isegi futuristlikele vaadetele.
• Tasuvuse määr on konkreetse kasumi jaoks soovitava investeeringu lihtne arvutamine. Nende sisendites saab teha muudatusi ja proovida mõista investeeritava summa suurust, et teenida konkreetset tootlust.
• Seda kasutatakse erinevate investeeringute võrdlemiseks ja selliste investeeringute tagamaade või nende eeliste mõistmiseks.
• See annab vastava üksikisiku või ettevõtte finantsseisundi tervikuna.

Järeldus

Tasuvuse määr on kõigi investeeringute ja nende tasuvusega seotud analüüside jaoks keskne terminoloogia. See aitab mitmel viisil, nagu eespool nägime, kuid ainult siis, kui see on õigesti arvutatud. Kuigi see näib lihtsa valemina, annab see tulemusi, mida on vaja mõne suurema otsuse tegemiseks - olgu see siis rahanduse või muude tagasipöördumisega seotud otsuste puhul. Seetõttu on täpse arvutuseni jõudmine väga oluline, kuna see moodustab kogu investeeringute, tuleviku planeerimise ja muude majandusega seotud otsuste aluse.