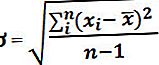seychellesartprojects.org

Mis on Macaulay kestus?

Macaulay kestus on aeg, mille investor võtab võlakirja investeeritud raha tagasi kupongide ja põhiosa tagasimaksmise kaudu. See ajavahemik on selle perioodi kaalutud keskmine, mille investor peaks investeerima väärtpaberisse, et investeeringu rahavoogude nüüdisväärtus vastaks võlakirja eest makstud summale.

Macaulay kestus on väga oluline tegur, mida tuleks enne võlainstrumendi ostmist arvesse võtta. See võib investoritele suuresti aidata valida turul saadaolevate fikseeritud tulumääraga väärtpaberite mitmekesiste komplektide hulgast. Kuna me kõik teame, et võlakirjade hinnad on pöördvõrdeliselt seotud intressimääradega, saavad investorid hea idee, millist võlakirja osta, kas pikema või lühema tähtajaga, kui nad teavad, millist kestust pakuvad erinevad kupongivõlakirjad koos prognoositud intressimäära struktuur.

Macaulay kestuse valem

Selle saab arvutada järgmise valemi abil:

Kus

• t = ajavahemik
• C = kupongimakse
• y = saagis
• n = perioodide arv
• M = tähtaeg
• Praegune võlakirja hind = rahavoogude nüüdisväärtus

Macaulay kestuse arvutamine näitega

Vaatame Macaulay kestuse näidet, et sellest paremini aru saada.

Selle Macaulay Duration Exceli malli saate alla laadida siit - Macaulay Duration Exceli mall

1000 dollari väärtuses võlakiri maksab 8% kupongimäära ja lõpeb nelja aastaga. Kupongi määr on 8% aastas koos poolaastase maksega. Võime eeldada, et tekivad järgmised rahavood.

• 6 kuud: 40 dollarit
• 1 aasta: 40 dollarit
• 1,5 aastat: 40 dollarit
• 2 aastat: 40 dollarit
• aastat: 40 dollarit
• 3 aastat: 40 dollarit
• 3,5 aastat: 40 dollarit
• 4 aastat: 1040 dollarit

Arvutage Macaulay kestus

Lahendus:

Ülaltoodud teabe põhjal saame arvutada allahindlusteguri. Diskontoteguri tuletamiseks võime kasutada järgmist poolaasta intressivalemit. 1 / (1 + r) n, kus r on kupongimäär ja n on liitperioodide arv.

Soodustustegur

Soodustustegurite arvutamine 6 kuuks on -

6 kuu diskontotegurid = 1 / (1 + 8% / 2)

Soodustustegurid = 0,9615

Samamoodi saame arvutada allahindlusteguri aastateks 1 kuni 4.

Rahavoogude nüüdisväärtus

Kuu kuu rahavoogude nüüdisväärtus on -

Nüüd peame rahavoogude nüüdisväärtuse saamiseks korrutama iga perioodi rahavood vastava diskontoteguriga.

Rahakäibe nüüdisväärtus 6 kuud: 1 x 40 USD x 0,9615

Rahavoogude praegune väärtus = 38,46 dollarit

Samamoodi saame arvutada rahavoo nüüdisväärtuse 1. kuni 4. aastaks.

Macaulay Kestus

Macaulay kestuse arvutamine on -

• Praegune võlakirja hind = kõigi rahavoogude PV 6079,34
• Macaulay kestus = 6079,34 dollarit / 1000 dollarit = 6,07934

Macaulay kestuse üksikasjalikuks arvutamiseks võite viidata ülaltoodud Exceli mallile.

Kestuse kasutamise eelised

Kestus mängib olulist rolli, aidates investoritel mõista saadaoleva fikseeritud tulumääraga väärtpaberi riskitegurit. Nii nagu aktsiate riski mõõdetakse kõrvalekaldega keskmisest või lihtsalt tuletades väärtpaberi beeta, hinnatakse fikseeritud tulumääraga instrumentide riski rangelt instrumendi Macaulay kestuse järgi.

Instrumentide Macaulay mõistmine ja võrdlemine võib teie fikseeritud tulumääraga portfelli sobiva valiku tegemisel palju aidata.

Kestuse kasutamise tagasilöögid

Kestus on optsioonivaba võlakirja hinnamuutuste hea ligikaudne arv, kuid see on hea ainult väikeste intressimäärade muutuste korral. Kui intressimäärade muutused muutuvad suuremaks, muutub võlakirja hinna ja tootluse suhte kumerus olulisemaks ehk teisisõnu sisaldab hinnamuutuste lineaarne hinnang, näiteks kestus, vigu.

Tegelikult ei ole võlakirja hinna ja tootluse suhe lineaarne, vaid kumer. See kumerus näitab, et tegelike ja hinnanguliste hindade erinevus suureneb, kui tootlus tõuseb. See tähendab, et hinnangulise hinna suurenev viga on tingitud tegeliku hinnakõvera kumerusest. Seda tuntakse kui kumeruse astet.

Alumine joon

Macaulay teadmised kestuse kohta on fikseeritud tulumääraga instrumentide tulevase tootluse väljaselgitamisel esmatähtsad, seetõttu on investoritele, eriti riskikartlikele investoritele, väga soovitatav hinnata ja võrrelda erinevate võlakirjade pakutavat kestust, et jõuda minimaalsesse dispersioonisegusse ja tõmmata maksimaalne tasub võimalikult vähese riskiga. Samuti tuleks enne ostuotsuse tegemist kaaluda intressimäära tegurit.