Piirhüvitis (määratlus, valem) Arvutusnäited
Mis on marginaalne kasu?
Piirhüvitis aitab organisatsioonil välja selgitada tarbimisest saadava kasu optimaalse taseme ja arvutab oma toote / teenuse hinnangulise koguse, mida turg nõuab, suurendades seeläbi ettevõtte juhtimise kulutasuvust. Lühidalt, see aitab organisatsioonil oma äri tõhusamalt juhtida.
Piirkasu on järkjärguline kasv tarbija kasuks, mis tuleneb ostetud toote või teenuse täiendava ühiku suurenenud tarbimisest. Tarbija rahulolu kipub tarbimise kasvades vähenema.
Piirhüvitise valem
Piirhüvitise valem = kogukasu muutus / tarbitud ühikute arvu muutus
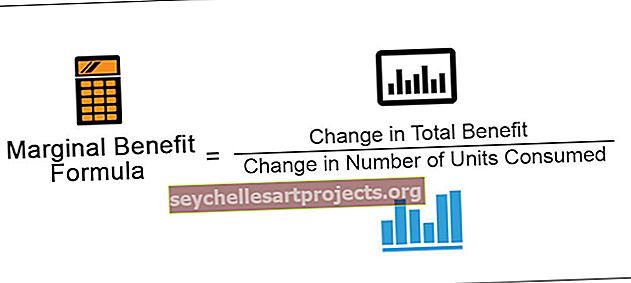
Hüvitiste muutus
See osa hõlmab kogukasu muutust ja tuletatakse praeguse tarbimise kogukasu eelmisest tarbimisest lahutades. Arendagem paremat mõistmist järgmise näite abil. Oletame, et tarbides esimest banaani, saab tarbija kasu 10 ühikust, teine banaan toob aga kasu kokku 18. Selleks, et jõuda teise ja esimese banaani koguhüvitise muutuseni, peame maha arvestama banaani koguhüvitise. esimene banaan teisest banaanist. Tulemuseks on hüvitise kogusumma 8 (18 - 10).
Tarbitud ühikute arvu muutus
See osa hõlmab tarbitud ühikute arvu muutuse arvutamist. Selle tuletamiseks lahutatakse varem tarbitud ühikust praegu tarbitava ühiku kogus. Teisest ja esimesest banaanist tarbitud ühikute muutus on 1 (2 - 1).
Mõlema osa arvutamisel saadakse marginaalne kasu jagades kogu hüvitise muutus tarbitud ühikute arvu erinevusega.
Näited
Selle Marginal Benefit Formula Exceli malli saate alla laadida siit - Marginal Benefit Formula Exceli mallNäide 1
Oletame, et tarbija Harry ostab ja tarbib jäätist, olgu jäätisest saadav kasu 50 ühikut. Harry tarbib veel kolm jäätist. 2., 3. ja 4. jäätise kasu on 40, 35 ja 25. Arvutage marginaalne kasu jäätise 1. ja 2. ning 1. ja 3. ühiku kohta.
Lahendus:
Kasutage arvutamiseks antud andmeid

1. ja 2. jäätise arvutamise saab teha järgmiselt:

1. ja 2. jäätis on (50–40) / (2. – 1. Üksus)

1. ja 2. jäätise marginaalne kasu = 10
3. ja 1. jäätise arvutamise saab teha järgmiselt:

3. ja 1. jäätise eelis on (50–35) / (3. – 1. Üksus)
3. ja 1. jäätise eelised on -

3. ja 1. jäätise marginaalne kasu = 7,5
Näide 2
Hr Peter tegeleb tee müümisega. Varasemate müügikogemuste põhjal on ta hinnanud oma tee tarbimisest tulenevat kasu, mida mainiti järgmiselt:

Iga täiendava müüdud ühiku kohta peate arvutama marginaalse kasu.
Lahendus:

Ühe tee koguse marginaalne kasu = (300-0) / (1-0)

Samamoodi saame arvutada ülejäänud tee koguse marginaalse kasu.

Näide # 3
Oletame, et hr Harry müüb jäätist hinnaga 10 dollarit. Muutuv valmistamiskulu on 5 dollarit ühiku kohta. Nii jääb brutokasum 5 dollarit ühiku kohta. (Püsikulusid ignoreeritakse lihtsuse huvides).
Lahendus:

Pühapäeval müüb ta 100 ühikut, mille brutokasum on 5 dollarit x 100 ühikut ehk 500 dollarit.
Kuid müügi suurendamiseks otsustab Harry hinna langetada 9 dollarini. Selle hinnaga teeniksite brutokasumit 4 dollarit ühiku kohta.
Alandatud hindade tõttu suureneb müügimaht 180 ühikuni. Esimesed 100 tarbijat nõustusid maksma 10 dollarit, seega on veelgi õnnelikumad maksta 9 dollarit. Lisaks liitus veel 75 klienti, kes on nõus maksma 9 dollarit. Brutokasum on nüüd 720.
Arvutamist saab teha järgmiselt:

Piirkasu saab olema (720–500 dollarit) / (180 ühikut - 100 ühikut)

Lõpliku müügihinna võib müüja arvutada oma äri mõjutavate erinevate tegurite põhjal.
Asjakohasus ja kasutusalad
- Kasu optimaalse taseme põhjal võib organisatsioon koostada eelarve toodetava koguse jaoks.
Võtmed kaasa
- Kliendi saadud hüvede arvu muutus, suurendades tarbimist ühe täiendava kauba / teenuse ühiku võrra, on marginaalne eelis.
- See on pöördvõrdeliselt seotud tarbimisega, st tarbimise suurenemisega marginaalne kasu väheneb.
- Kui toodang või teenus suureneb, on kulude muutus tootmise piirmaksumus.
- See aitab kindlaks määrata nõutava teenuse või toote kõige tõhusama taseme.
- Samuti aitab see saavutada mastaabisäästu.