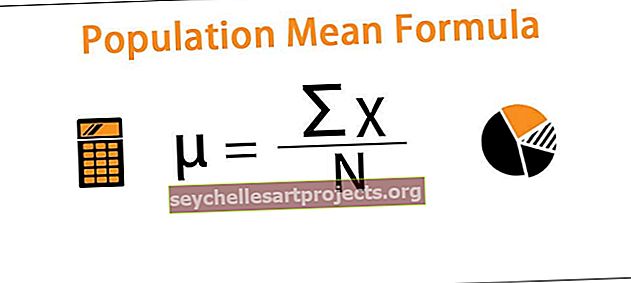Normaliseerimise valem | Samm-sammuline juhend koos arvutusnäidetega
Mis on normaliseerimise valem?
Statistikas viitab mõiste „normaliseerimine” andmekogumi vähendamisele nii, et normaliseeritud andmed jäävad vahemikku 0–1. Sellised normaliseerimismeetodid aitavad võrrelda kahe või enama erineva andmekogumi vastavaid normaliseeritud väärtusi viisil et see välistab andmekogumite skaala varieerumise mõju, st suurte väärtustega andmekogumit saab hõlpsasti võrrelda väiksemate väärtustega andmekogumiga.
Normaliseerimise võrrand saadakse nii, et algselt lahutatakse normaliseeritavast muutujast minimaalne väärtus, seejärel lahutatakse maksimaalsest väärtusest minimaalne väärtus ja seejärel jagatakse eelmine tulemus viimasega.
Matemaatiliselt on normaliseerimise võrrand esitatud järgmiselt:
x normaliseeritud = ( x - x miinimum ) / ( x maksimaalne - x miinimum )
Normaliseerimisvalemi selgitus
Normaliseerimise arvutamise võrrandi saab tuletada järgmiste nelja lihtsa sammu abil:
1. samm: esiteks määrake andmekogumis minimaalne ja maksimaalne väärtus ning neid tähistatakse x miinimumi ja x maksimumiga .
2. samm: Seejärel arvutage andmekogumi vahemik, lahutades minimaalsest väärtusest maksimaalse väärtuse.
Vahemik = x maksimum - x miinimum
Samm 3: Järgmisena tehke kindlaks, kui palju rohkem väärtust on muutuja normaliseeritav miinimumväärtusest, lahutades muutujast minimaalse väärtuse, st x - x miinimum .
4. samm: lõpuks saadakse muutuja x normaliseerimise arvutamise valem , jagades 3. etapi avaldise 2. sammu avaldisega, nagu eespool näidatud.
Normaliseerimisvalemi näited (Exceli malliga)
Selle paremaks mõistmiseks vaatame normaliseerimise võrrandite lihtsaid ja täpsemaid näiteid.
Normaliseerimise valem - näide 1
Määrake normaliseeritud väärtus 11,69, st skaalal (0,1), kui andmete madalaim ja suurim väärtus on vastavalt 3,65 ja 22,78.
Eeltoodust oleme kogunud järgmise teabe.

Seetõttu arvutatakse normaliseerimisväärtus 11,69 järgmiselt:

- x (normaliseeritud) = (11,69-3,65) / (22,78-3,65)
Normaliseerimisväärtus 11,69 on -

- x (normaliseeritud) = 0,42
Antud andmekogumi väärtuse 11,69 saab teisendada skaalal (0,1) väärtuseks 0,42.
Normaliseerimise valem - näide 2
Võtame veel ühe näite andmekogumist, mis esindab 20 õpilase hiljutise loodusteadusliku testi käigus saadud hindeid. Esitage kõigi õpilaste testitulemused vahemikus 0 kuni 1 normaliseerimisvõtete abil. Testitulemused (100st) on järgmised:

Vastavalt antud testi skoorile
Kõrgeima testi hinde hindab õpilane 11, st x maksimaalne = 95 ja
Madalaima testi hinde hindab õpilane 6 ehk x miinimum = 37

Nii et õpilase 1 normaliseeritud hinde arvutamine on järgmine,

- Normaliseeritud õpilase skoor 1 = (78 - 37) / (95 - 37)
Normaliseeritud õpilase skoor 1

- 1. õpilase normaliseeritud skoor = 0,71
Sarnaselt oleme kõigi 20 õpilase punktisumma normaliseerimise arvutanud järgmiselt:
- 2. õpilase skoor = (65–37) / (95–37) = 0,48
- 3. õpilase skoor = (56 - 37) / (95 - 37) = 0,33
- 4. õpilase skoor = (87 - 37) / (95 - 37) = 0,86
- Õpilase 5 skoor = (91 - 37) / (95 - 37) = 0,93
- Õpilase 6 skoor = (37 - 37) / (95 - 37) = 0,00
- 7. õpilase skoor = (49 - 37) / (95 - 37) = 0,21
- Õpilase skoor 8 = (77 - 37) / (95 - 37) = 0,69
- Tudengi skoor 9 = (62 - 37) / (95 - 37) = 0,43
- Õpilase skoor 10 = (59 - 37) / (95 - 37) = 0,38
- 11. õpilase skoor = (95 - 37) / (95 - 37) = 1,00
- 12. õpilase skoor = (63–37) / (95–37) = 0,45
- Õpilase 13 skoor = (42 - 37) / (95 - 37) = 0,09
- Õpilase 14 skoor = (55 - 37) / (95 - 37) = 0,31
- Õpilase 15 skoor = (72 - 37) / (95 - 37) = 0,60
- Õpilase 16 skoor = (68 - 37) / (95 - 37) = 0,53
- Õpilase 17 skoor = (81 - 37) / (95 - 37) = 0,76
- Õpilase 18 skoor = (39 - 37) / (95 - 37) = 0,03
- Õpilase 19 skoor = (45 - 37) / (95 - 37) = 0,14
- Õpilase 20 skoor = (49 - 37) / (95 - 37) = 0,21
Nüüd joonistagem õpilaste normaliseeritud skoori graafik.

Normaliseerimise valemi kalkulaator
Saate kasutada seda normaliseerimisvalemi kalkulaatorit.
| X | |
| X miinimum | |
| X maksimaalselt | |
| X normaliseerus | |
| X normaliseeritud = |
|
|
Asjakohasus ja kasutamine
Normaliseerimise mõiste on väga oluline, kuna seda kasutatakse sageli erinevates valdkondades, näiteks reitingutes, kus normaliseerimise tehnikat kasutatakse erinevatel skaalal mõõdetud väärtuste kohandamiseks mõtteliselt levinud skaalaga (0 kuni 1). Normaliseerimise mõistet saab kasutada ka keerukamate ja keerukamate kohanduste jaoks, näiteks viia kogu korrigeeritud väärtuste tõenäosusjaotuse komplekt joondamisse või kvantiilide normaliseerimine, kus erinevate mõõtmete kvantiilid viiakse joondusse.
Samuti leiab see rakendust hariduslikus hindamises (nagu eespool näidatud), et viia õpilaste hinded vastavusse normaaljaotusega. Kuid see tehnika ei saa eriti hästi toime tulla kõrvalmõjudega, mis on selle üks peamisi piiranguid.
Selle Normalization Formula Exceli malli saate alla laadida siit - Normalization Formula Exceli mall