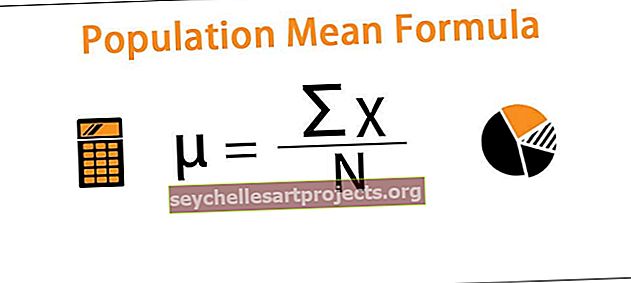seychellesartprojects.org

Viltuvormel on statistiline valem, mis arvutab antud muutujate hulga tõenäosusjaotuse ja võib olla nii positiivne, negatiivne kui ka määratlemata.

Viltuse arvutamise valem

Mõiste „viltu” viitab statistilisele mõõdikule, mida kasutatakse juhuslike muutujate tõenäosusjaotuse asümmeetria mõõtmiseks oma keskmise suhtes ja selle väärtus võib olla positiivne, negatiivne või määratlemata. Viltuse võrrandi arvutamine toimub jaotuse keskmise, muutujate arvu ja jaotuse standardhälbe põhjal.

Matemaatiliselt on viltuse valem esitatud järgmiselt:

kus

• X _i = juhuslik muutuja
• X = jaotuse keskmine
• N = muutujate arv jaotuses
• Ơ = standardjaotus

Viltuse arvutamine (samm-sammult)

• 1. samm: esiteks moodustage juhuslike muutujate andmete jaotus ja neid muutujaid tähistatakse tähega X _i .
• 2. samm: Järgmisena selgitage välja andmete jaotuses saadaolevate muutujate arv ja seda tähistatakse N-ga.
• 3. samm: Järgmisena arvutage andmete jaotuse keskmine, jagades kõigi andmete jaotuse juhuslike muutujate summa jaotuse muutujate arvuga. Jaotuse keskmist tähistatakse X-ga.

• 4. samm: Järgmisena määrake jaotuse standardhälve, kasutades iga muutuja hälbeid keskmisest, st X _i - X ja muutujate arvu jaotuses. Standardhälve arvutatakse vastavalt allpool näidatule.

• 5. samm: Lõpuks tehakse vildakuse arvutamine iga muutuja hälbe keskmise, mitme muutuja ja jaotuse standardhälbe põhjal, nagu allpool näidatud.

Näide

Selle Skewness Formula Exceli malli saate alla laadida siit - Skewness Formula Exceli mall

Võtame näiteks suvelaagri, kus 20 õpilast määrasid teatud tööd, mida nad rahateenimiseks kooli pikniku jaoks rahaliste vahendite saamiseks tegid. Erinevad õpilased teenisid aga erinevat summat. Allpool toodud teabe põhjal määrake õpilaste sissetulekute jaotuse viltu suvelaagri ajal.

Lahendus:

Järgnevalt on toodud andmed viltuse arvutamiseks.

Muutujate arv, n = 2 + 3 + 5 + 6 + 4 = 20

Arvutame iga intervalli keskpunkti

• (0 dollarit + 50 dollarit) / 2 = 25 dollarit
• (50 dollarit + 100 dollarit) / 2 = 75 dollarit
• (100 dollarit + 150 dollarit) / 2 = 125 dollarit
• (150 dollarit + 200 dollarit) / 2 = 175 dollarit
• (200 dollarit + 250 dollarit) / 2 = 225 dollarit

Nüüd saab jaotuse keskmise arvutada järgmiselt:

Keskmine = ($ 25 * 2 + $ 75 * 3 + $ 125 * 5 + $ 175 * 6 + $ 225 * 4) / 20

Keskmine = 142,50 dollarit

Iga muutuja hälvete ruudud saab arvutada järgmiselt:

• (25–142,5 dollarit) 2 = 13806,25
• (75–142,5 dollarit) 2 = 4556,25
• (125–142,5 dollarit) 2 = 306,25
• (175 dollarit - 142,5 dollarit) 2 = 1056,25
• (225–142,5 dollarit) 2 = 6806,25

Nüüd saab standardhälbe arvutada järgmise valemi abil:

ơ = [(13806,25 * 2 + 4556,25 * 3 + 306,25 * 5 + 1056,25 * 6 + 6806,25 * 4) / 20] 1/2

ơ = 61,80

Iga muutuja kõrvalekallete kuubikud saab arvutada järgmiselt:

• (25 dollarit - 142,5 dollarit) 3 = -1622234,4
• (75 dollarit - 142,5 dollarit) 3 = -307546,9
• (125 dollarit - 142,5 dollarit) 3 = -5359,4
• (175 dollarit - 142,5 dollarit) 3 = 34328,1
• (225 dollarit - 142,5 dollarit) 3 = 561515,6

Seetõttu arvutatakse jaotuse kalduvus järgmiselt,

= (-1622234.4 * 2 + -307546,9 * 3 + -5359,4 * 5 + 34328,1 * 6 + 561515,6 * 4) / [(20-1) * (61,80) 3]

Viltus saab olema -

Viltusus = -0,39

Seetõttu on jaotuse kalduvus -0,39, mis näitab, et andmete jaotus on ligikaudu sümmeetriline.

Viltuse valemi asjakohasus ja kasutusalad

Nagu juba käesolevas artiklis näha, kasutatakse andmete jaotuse sümmeetria kirjeldamiseks või hindamiseks viltu. See on riskihalduse, portfellihalduse, kauplemise ja optsioonide hinnastamise seisukohast väga oluline. Mõõtu nimetatakse „viltuseks“, kuna joonisel olev graafik annab viltuse kuva. Positiivne viltus näitab, et äärmuslikud muutujad on suuremad kui viltused, on andmete jaotus selline, et see suurendab keskmist väärtust viisil, mis on suurem kui mediaan, mille tulemuseks on viltune andmekogum. Teisest küljest näitab negatiivne kaldenurk, et äärmuslikud muutujad on väiksemad, mis langetab keskmise väärtuse, mille tulemuseks on keskmine mediaanist suurem. Niisiis tuvastab viltus sümmeetria puudumise või asümmeetria ulatuse.