seychellesartprojects.org

Mis on R-ruut (R2) regressioonis?

R-ruut (R2) on oluline statistiline mõõde, mis on regressioonimudel, mis esindab sõltuva muutuja statistilise erinevuse või varieeruvuse osakaalu, mida saab seletada sõltumatu muutuja või muutujate abil. Lühidalt, see määrab, kui hästi andmed sobivad regressioonimudeliga.

R ruudukujuline valem

R ruutu arvutamiseks peate määrama korrelatsioonikordaja ja seejärel tulemuse ruutu.

R ruuduline valem = r2

Kus r saab korrelatsioonikordaja arvutada allpool:

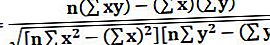
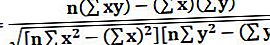
Kus

• r = korrelatsioonikordaja
• n = arv antud andmekogumis
• x = esimene muutuja kontekstis
• y = teine ​​muutuja

Selgitus

Kui nende kahe muutuja vahel on suhe või korrelatsioon, mis võib olla lineaarne või mittelineaarne, näitab see, kas sõltumatu muutuja väärtus on muutunud, siis tõenäoliselt muutub teine ​​sõltuv muutuja väärtuses, näiteks lineaarselt või mittelineaarselt. lineaarselt.

Valemi lugejaosa viib läbi testi, kas nad liiguvad koos, ja eemaldab nende individuaalsed liikumised ning nende mõlema koos liikumise suhtelise tugevuse ja valemi nimetaja osa skaalab lugeja, võttes ruutväärtuse erinevuste korrutise ruutjuure. muutujad nende ruudulistest muutujatest. Ja kui selle tulemuse ruutu panna, saame R ruutu, mis pole midagi muud kui määramistegur.

Näited

Selle R Ruudulise valemi Exceli malli saate alla laadida siit - R ruutu valemi Exceli mall

Näide 1

Mõelge järgmisele kahele muutujale x ja y, teil on vaja arvutada R ruut regressioonis.

Lahendus:

Kasutades ülalnimetatud valemit, peame kõigepealt arvutama korrelatsioonikordaja.

Meil on kõik ülaltoodud tabeli väärtused n = 4.

Joonise saamiseks sisestame nüüd valemis olevad väärtused.

r = (4 * 26 046,25) - (265,18 * 326,89) / √ [(4 * 21 274,94) - (326,89) 2] * [(4 * 31 901,89) - (326,89) 2]

r = 17 501,06 / 17 512,88

Korrelatsioonikordaja on

r = 0,99932480

Seega arvutatakse järgmiselt,

r2 = (0,99932480) 2

R ruudukujuline valem regressioonis

r2 = 0,998650052

Näide 2

India, arengumaad, soovib teha sõltumatu analüüsi, kas toornafta hinna muutused on mõjutanud tema ruupia väärtust. Järgneb Brenti toornafta hinna ja ruupia hindamise ajalugu nii dollarite suhtes, mis valitsesid keskmiselt nendel aastatel allpool.

India keskpank RBI on pöördunud teie poole, et järgmisel koosolekul esitada sama kohta ettekanne. Tehke kindlaks, kas toornafta liikumine mõjutab ruupia dollari liikumist?

Lahendus:

Kasutades ülaltoodud korrelatsiooni valemit, saame kõigepealt arvutada korrelatsioonikordaja. Keskmise toornafta hinna käsitlemine ühe muutujana ütleb x ja teise ruupia ühe dollari muutujana käsitlemine y-na.

Meil on kõik ülaltoodud tabeli väärtused n = 6.

Joonise saamiseks sisestame nüüd valemis olevad väärtused.

r = (6 * 23592,83) - (356,70 * 398,59) / √ [(6 * 22829,36) - (356,70) 2] * [(6 * 26529,38) - (398,59) 2]

r = -620,06 / 1715,95

Korrelatsioonikordaja on

r = -0,3614

Seega arvutatakse järgmiselt,

r2 = (-0,3614) 2

R ruudukujuline valem regressioonis

r2 = 0,1306

Analüüs: näib, et toornafta hinna muutuste ja India ruupia hinna muutuste vahel on väike seos. Toornafta hinna tõustes mõjutavad ka India ruupia muutused. Kuid kuna R ruut on ainult 13%, seletavad toornafta hinna muutused India ruupia muutusi vähem ja India ruupia võib muutuda ka muudes muutujates, mida tuleb arvestada.

Näide # 3

XYZ laboratoorium uurib pikkust ja kaalu ning on huvitatud teadmisest, kas nende muutujate vahel on mingisugune seos. Pärast 5000 kategooria valimi kogumist iga kategooria kohta ja tulid välja selle konkreetse rühma keskmise kaalu ja keskmise pikkusega.

Allpool on üksikasjad, mille nad on kogunud.

Peate arvutama R ruutu ja tegema järelduse, kui see mudel selgitab kõrguse erinevusi, mis mõjutavad kaalu erinevusi.

Lahendus:

Kasutades ülaltoodud korrelatsiooni valemit, saame kõigepealt arvutada korrelatsioonikordaja. Kui käsitletakse kõrgust ühe muutujana, öeldakse x ja kaalu käsitletakse teise muutujana y-na.

Meil on kõik ülaltoodud tabeli väärtused n = 6.

Joonise saamiseks sisestame nüüd valemis olevad väärtused.

r = (7 * 74 058,67) - (1031 * 496,44) / √ [(7 * 153595 - (1031) 2] * [(7 * 35793,59) - (496,44) 2]

r = 6581,05 / 7075,77

Korrelatsioonikordaja on

Korrelatsioonikordaja (r) = 0,930

Seega arvutatakse järgmiselt,

r2 = 0,865

Analüüs: korrelatsioon on positiivne ja tundub, et pikkuse ja kaalu vahel on teatud seos, kuna pikkus suurendab ka inimese kaalu. Kui R2 soovitab, et 86% pikkuse muutustest on seotud kaalu muutustega ja 14% on seletamatud.

Asjakohasus ja kasutusalad

R ruutu olulisus regressioonis on selle võime leida tulevaste sündmuste tõenäosus etteantud prognoositud tulemuste või tulemuste piires. Kui mudelile lisatakse rohkem proove, näitaks koefitsient uue punkti või uue andmekogumi joonele kukkumise tõenäosust või tõenäosust. Isegi kui mõlemal muutujal on tugev seos, ei tõenda määramine põhjuslikkust.

Mõned ruumid, kus R-ruutu enamasti kasutatakse, on investeerimisfondide tootluse jälgimiseks, riskifondide riski jälgimiseks, et teha kindlaks, kui hästi aktsia turuga liigub, kus R2 soovitab, kui palju aktsia liikumistest saab selgitada turu liikumine.