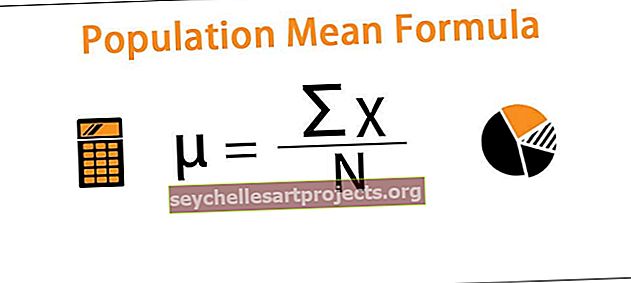seychellesartprojects.org

Binomiaaljaotuse arvutamise valem

Binomiaaljaotuse valemit kasutatakse x edukuse saamise tõenäosuse arvutamiseks binoomkatse n katses, mis on sõltumatud ja tõenäosus tuletatakse katsete arvu ja nCx-ga esindatud õnnestumiste kombinatsiooniga, korrutades saadud edukuse tõenäosusega edukuse arvu, mida esindab px, võimsus, mis korrutatakse veel ebaõnnestumise tõenäosusega, mis on suurendatud edukuse arvu ja katsete arvu (1-p) nx vahelise erinevuse võimsuseni.

B binoomkatse n sõltumatu katse korral x õnnestumise saamise tõenäosuse annab järgmine binoomjaotuse valem:

P (X) = _n C _x px (1-p) nx

kus p on edukuse tõenäosus

Ülaltoodud võrrandis kasutatakse _n C _x , mis pole midagi muud kui kombinatsioonide valem. Kombinatsioonide arvutamise valem on esitatud _n C _x = n! / x! (nx)!  kus n tähistab üksuste arvu (sõltumatud proovid) ja x tähistab korraga valitud üksuste arvu (õnnestumised).

Juhul kui n = 1 binoomjaotuses, on jaotus tuntud kui Bernoulli jaotus. Binoomse jaotuse keskmine on np. Binoomjaotuse dispersioon on np (1-p).

Binomiaaljaotuse arvutamine (samm-sammult)

Binoomse jaotuse arvutamise saab tuletada järgmise nelja lihtsa toimingu abil:

• 1. samm: arvutage katsete ja õnnestumiste arvu kombinatsioon. _N C _x valem on see, kus n! = n * (n-1) * (n-2). . . * 2 * 1. Numbri n jaoks võib n faktori kirjutada järgmiselt: n! = n * (n-1)! Näiteks 5! on 5 * 4 * 3 * 2 * 1
• 2. samm: arvutage edukuse tõenäosus pikslitega õnnestumiste arvu võimsuseni.
• 3. samm: arvutage ebaõnnestumise tõenäosus edukuse arvu ja katsete arvu vahelise erinevuse suuruseks. Ebaõnnestumise tõenäosus on 1-p. Seega viitab see (1-p) nx saamisele
• 4. samm: saate teada 1., 2. ja 3. etapis saadud tulemuste korrutis.

Näited

Selle Binomial Distribution Formula Exceli malli saate alla laadida siit - Binomial Distribution Formula Exceli mall

Näide 1

Katsete arv (n) on 10. Edu õnnestumise tõenäosus (p) on 0,5. Tehke binoomjaotuse arvutamine, et arvutada täpselt 6 õnnestumise tõenäosus.

Lahendus:

Binoomjaotuse arvutamiseks kasutage järgmisi andmeid.

Binoomse jaotuse saab arvutada järgmiselt:

P (x = 6) oli ₁₀ C ₆ * (0,5) 6 (1-0,5) 06/10

                = (10! / 6! (10-6)!) * 0,015625 * (0,5) 4

               = 210 * 0,015625 * 0,0625

Tõenäosus saada täpselt 6 edulood  on uskumuse

P (x = 6) = 0,205

Täpselt 6 õnnestumise tõenäosus on 0,2051

Näide 2

Kindlustusseltsi juht läbib tema all töötavate kindlustusmüüjate poolt müüdud kindlustuspoliiside andmeid. Ta leiab, et 80% liikluskindlustust ostvatest inimestest on mehed. Ta soovib teada saada, et kui juhuslikult valitakse 8 liikluskindlustuse omanikku, siis milline oleks tõenäosus, et neist täpselt 5 on mehed.

Lahendus: kõigepealt peame välja selgitama, mis on n, p ja x.

Binoomse jaotuse saab arvutada järgmiselt:

P (x = 5) = ₈ C ₅ * (0,8) 5 (1-0,8) 8-5

               = (8! / 5! (8-5)!) * 0,32768 * (0,2) 3

              = 56 * 0,32768 * 0,008

Tõenäosus täpselt 5 edulood  on uskumuse

P (x = 5) = 0,146000064

Täpselt 5 liikluskindlustuse omaniku tõenäosus olla mees on 0,144680064.

Näide # 3

Haigla juhtkond on põnevil uue vähihaigete ravimi kasutuselevõtu üle, kuna võimalus, et inimene saab seda edukalt ravida, on väga suur. Patsiendi tõenäosus ravimiga edukalt ravida on 0,8. Ravimit antakse 10 patsiendile. Leidke tõenäosus, et see ravib edukalt 9 või enamat patsienti.

Lahendus: kõigepealt peame välja selgitama, mis on n, p ja x.

Peame leidma tõenäosuse, et see ravib edukalt 9 või enamat patsienti. Seega ravib see edukalt kas 9 või 10 patsienti

x (arv, mille korral peate leidma tõenäosuse) = 9 või x = 10

Peame leidma P (9) ja P (10)

B (b = 9) leidmiseks võib binoomjaotuse arvutada järgmiselt:

P (x = 9) = ₁₀ C ₉ * (0,8) 9 (1-0,8) 09/10

               = (10! / 9! (10-9)!) * 0,1334217728 * (0,2)

               = 10 * 0,1334217728 * 0,2

Tõenäosus 9 Patsiendid  on uskumuse

P (x = 9) = 0,2684

B (b = 10) leidmiseks võib binoomjaotuse arvutada järgmiselt:

P (x = 10) = ₁₀ C ₁₀ * (0,8) 10 (1-0,8) 10-10

                  = (10! / 10! (10-10)!) * 0,107374182 * (0,2) 0

                  = 1 * 0,107374182 *

Tõenäosus 10 Patsiendid  on uskumuse

P (x = 10) = 0,1074

Seetõttu P (x = 9) + P (x = 10) = 0,268 + 0,1074

= 0,3758

Seega on 9 või enama patsiendi tõenäosus seda ravimit ravida 0,375809638.  

Binomiaaljaotuse kalkulaator

Võite kasutada järgmist binoomjaotuse kalkulaatorit.

n
lk
x
Binomiaaljaotuse valem =

Binomiaaljaotuse valem =	n C x * px * (1 -p) nx
	0 C 0 * 0 0 * (1-0) 0 - 0 =	0

Asjakohasus ja kasutamine

• On ainult kaks tulemust
• Iga tulemuse tõenäosus jääb proovist proovini konstantseks
• Katsetusi on kindel arv
• Iga kohtuprotsess on sõltumatu, st välistab üksteist
• See annab meile edukate tulemuste võimaliku arvu sagedusjaotuse teatud arvu katsete korral, kus kõigil nendel antud katsetel on sama edukuse tõenäosus.
• Iga binoomkatses tehtud katse võib anda vaid kaks võimalikku tulemust. Seega on nimi "binomiaalne". Ühte neist tulemustest nimetatakse edukuseks ja teist ebaõnnestumiseks. Näiteks võivad haiged inimesed ravile reageerida või mitte.
• Samamoodi võib mündi viskamisel olla ainult kahte tüüpi tulemusi: pea või saba. Binoomjaotus on statistikas kasutatav diskreetne jaotus, mis erineb pidevast jaotusest.

Binoomkatse näide on mündi viskamine, ütleme kolm korda. Kui keerame münti, on võimalikud ainult 2 tulemust - pead ja sabad. Iga tulemuse tõenäosus on 0,5. Kuna münti visatakse kolm korda, on fikseeritud proovide arv, mis on 3. Iga viske tõenäosust muud visked ei mõjuta.

Binomiaaljaotus leiab oma rakendused sotsiaalteaduste statistikas. Seda kasutatakse dihhotoomsete tulemuste muutujate mudelite väljatöötamiseks, kus on kaks tulemust. Selle näiteks on see, kas valimised võidaksid vabariiklased või demokraadid.

Binomiaaljaotuse valem Excelis (Exceli malliga)

Saurabh sai binomiaaljaotuse võrrandist teada koolis. Ta soovib oma õega kontseptsiooni arutada ja temaga kihlvedusid sõlmida. Ta arvas, et viskab erapooletu mündi 10 korda. Ta tahab panustada 100 dollarit, kui saab 10 viskega täpselt 5 saba. Selle kihlveo eesmärgil soovib ta arvutada tõenäosuse saada 10 viskega täpselt 5 saba.

Lahendus: kõigepealt peame välja selgitama, mis on n, p ja x.

Binoomse jaotuse jaoks on sisseehitatud valem Excel, mis on

See on BINOM.DIST (õnnestumiste, katsete arv, õnnestumise tõenäosus, FALSE).

Selle binoomjaotuse näide oleks järgmine:

= BINOM.DIST (B2, B3, B4, FALSE), kus lahter B2 tähistab õnnestumiste arvu, lahter B3 tähistab katsete arvu ja lahter B4 edukuse tõenäosust.

Seetõttu arvutatakse binoomjaotuse arvutamine

P (x = 5) = 0,24609375

Tõenäosus saada täpselt 5 saba 10 viskega on 0,24609375

Märkus: FALSE tähistab ülaltoodud valemis tõenäosuse massifunktsiooni. See arvutab välja tõenäosuse, et n sõltumatust katsest õnnestub täpselt n edukust. TRUE tähistab kumulatiivset jaotusfunktsiooni. See arvutab välja tõenäosuse, et n sõltumatust katsest saab maksimaalselt x edu.