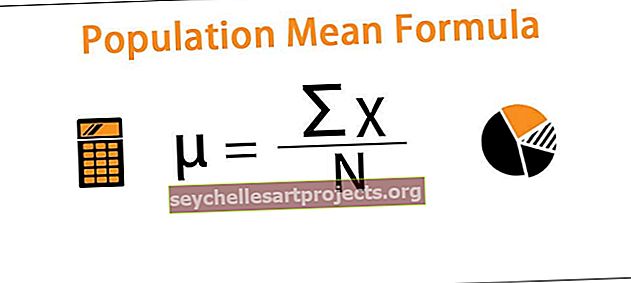seychellesartprojects.org

Mis on standardne veavalem?

Standardviga on määratletud kui viga, mis tekib valimi jaotuses statistilise analüüsi tegemisel. Põhimõtteliselt on see standardhälbe variant, kuna mõlemad mõisted vastavad levimismõõdudele. Kõrge standardviga vastab võetud valimi andmete suuremale levikule. Standardvea valemi arvutamine toimub valimi jaoks, samas kui standardhälve määratakse populatsiooni jaoks.

Seetõttu väljendatakse standardviga keskmises ja määratakse kindlaks vastavalt järgmiselt kirjeldatud seosele:

σ _͞x = σ / √n

Siin,

• Standardviga on väljendatud σ _͞x .
• Populatsiooni standardhälvet väljendatakse σ.
• Muutujate arv valimis on väljendatud n-na.

Statistilises analüüsis peetakse keskseks mõõdupuuks keskmist, mediaani ja režiimi. Kui standardhälve, dispersioon ja standardviga keskmises, klassifitseeritakse varieeruvuse näitajatena. Prooviandmete keskmise vea standardviga on otseselt seotud suurema populatsiooni standardhälbega ja pöördvõrdeline või seotud valimi moodustamiseks võetud arvu muutuja ruutjuurega. Seega, kui valimi suurus on väike, võib olla võrdne tõenäosus, et ka standardviga on suur.

Selgitus

Keskmise standardvea valemit saab selgitada järgmiste sammudega:

• 1. samm: esiteks tuvastage ja korraldage valim ning määrake muutujate arv.
• 2. samm: järgmisena valimi keskmine keskmine, mis vastab valimis olevate muutujate arvule.
• 3. samm: Seejärel määrake proovi standardhälve.
• 4. samm: Seejärel määrake valimisse võetud muutujate arvu ruutjuur.
• 5. samm: jagage nüüd 3. etapis arvutatud standardhälve 4. etapis saadud väärtusega, et saada standardviga.

Standardvea valemi näide

Allpool on toodud standardvea arvutamise valeminäited.

Selle standardse veavalemi Exceli malli saate alla laadida siit - standardvea valemi Exceli mall

Näide 1

Võtame näiteks aktsia ABC. 30 aasta jooksul oli aktsia dollari keskmine tootlus 45 dollarit. Täheldati, et aktsia andis tootlust standardhälbega 2 dollarit. Aidake investoril arvutada aktsia ABC pakutava keskmise tootluse üldine standardviga.

Lahendus:

Standardvea arvutamine on järgmine -

• σ _͞x = σ / √n
• = 2 dollarit / √30
• = 2 dollarit / 5,4773

Standardviga on,

• σ _͞x = 0,3651 dollarit

Seetõttu pakub investeering investorile dollari standardviga keskmiselt 0,36515 dollarit, kui ta on 30 aastat olnud aktsia ABC positsioonil. Kui aktsiat hoitakse aga kõrgema investeerimishorisondi jaoks, väheneks dollari keskmise standardviga märkimisväärselt.

Näide 2

Võtame näiteks investori, kes on aktsiatelt XYZ saanud järgmist tootlust: -

Aidake investoril arvutada XYZ aktsia pakutava keskmise tootluse üldine standardviga.

Lahendus:

Kõigepealt määrake allpool toodud tulude keskmine keskmine: -

• ͞X = (x1 + x2 + x3 + x4) / aastate arv
• = (20 + 25 + 5 + 10) / 4
• = 15%

Nüüd määrake tulude standardhälve, nagu allpool näidatud: -

• σ = √ ((x1-͞X) 2 + (x2-͞X) 2 + (x3-͞X) 2 + (x4-͞X) 2) / √ (aastate arv -1)
• = √ ((20-15) 2 + (25-15) 2 + (5-15) 2 + (10-15) 2) / √ (4-1)
• = (√ (5) 2 + (10) 2 + (-10) 2 + (-5) 2) / √ (3)
• = (√25 + 100 + 100 + 25) / √ (3)
• = √250 / √ 3
• = √83.3333
• = 9,1287%

Nüüd on standardvea arvutamine järgmine,

• σ _͞x = σ / √n
• = 9.128709 / √4
• = 9.128709 / 2

Standardviga on,

• σ _͞x = 4,56%

Seetõttu pakub investeering investorile 4 aasta jooksul aktsia XYZ positsiooni püsimisel dollari standardviga keskmiselt 4,56%.

Standardne veakalkulaator

Võite kasutada järgmist kalkulaatorit.

σ
n
Standardne veavalem

Standardvea valem =	σ = √ n
	0 = 0 √ 0

Asjakohasus ja kasutamine

Standardviga kipub olema kõrge, kui analüüsiks võetud valimi suurus on väike. Valim võetakse alati suuremast populatsioonist, mis hõlmab suuremat suurust muutujaid. Statistik aitab alati välja selgitada valimi keskmise usaldusväärsuse populatsiooni keskmise suhtes.

Suur standardviga ütleb statistikule, et valim ei ole populatsiooni keskmise suhtes ühtlane ja valimis on populatsiooni osas suuri erinevusi. Samamoodi ütleb väike standardviga statistikule, et valim on populatsiooni keskmise suhtes ühtlane ja valimis ei ole populatsiooni suhtes varieeruvaid muutusi või need on väikesed.

Seda ei tohiks segada standardhälbega. Standardhälve arvutatakse kogu populatsiooni kohta. Standardviga seevastu määratakse valimi keskmise jaoks.

Exceli standardvea valem

Võtame nüüd Exceli näite, et illustreerida standardvea valemi kontseptsiooni allpool Exceli mallis. Oletame, et kooli juhtkond soovib määrata standardvea jalgpallurite pikkuse keskmise suhtes.

Valim sisaldab järgmisi väärtusi:

Aidake administratsioonil standardviga keskmiselt hinnata.

1. samm: määrake keskmine, nagu allpool näidatud: -

2. samm: määrake standardhälve, nagu allpool näidatud: -

3. samm: määrake keskmise vea standardviga, nagu allpool näidatud: -

Seetõttu on jalgpallurite keskmise vea keskmine väärtus 1,846 tolli. Juhtkond peaks tähele panema, et see on märkimisväärselt suur. Seetõttu ei ole analüüsiks võetud valimi andmed ühetaolised ja neil on suur dispersioon.

Juhtkond peaks jalgpallimeeskonna keskmise pikkuse tasakaalustamiseks kas väiksemad mängijad välja jätma või lisama mängijad, kes on märkimisväärselt pikemad, asendades need väiksemate kõrgustega isikutega võrreldes eakaaslastega.