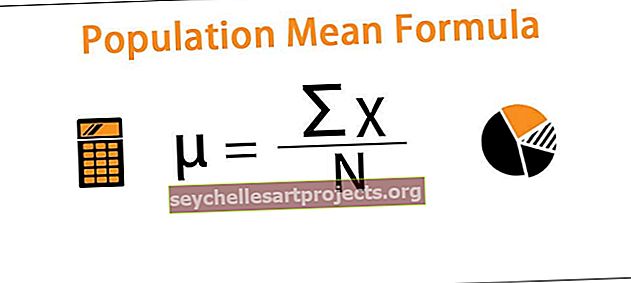seychellesartprojects.org

Statistika mediaani arvutamise valem

Keskmine valem statistikas viitab valemile, mida kasutatakse antud andmekogumis keskmise numbri määramiseks, mis on järjestatud kasvavas järjekorras ja vastavalt valemile lisatakse andmekogumis olevate üksuste arv ühele ja siis jagatakse tulemused kahega, et tuletada mediaanväärtuse kohast, st kindlaksmääratud positsioonile paigutatud number on mediaanväärtus.

See on vahend arvulise andmekogumi keskme mõõtmiseks. See võtab suure hulga andmeid kokku üheks väärtuseks. Seda saab määratleda numbrirühma keskmise numbrina, mis on järjestatud kasvavas järjekorras. Teisisõnu, mediaan on arv, millel oleks sama arv numbreid nii eespool kui ka allpool määratletud andmegrupis. See on statistikas ja tõenäosusteoorias tavaliselt kasutatav andmekogumite mõõdik.

Mediaan = {(n + 1) / 2}

kus 'n' on andmekogumi üksuste arv ja 'th' tähistab (n) numbrit.

Keskmine arvutus (sammhaaval)

• 1. samm: kõigepealt sorteerige numbrid kasvavas järjekorras. Numbrid on väidetavalt kasvavas järjekorras, kui see on paigutatud selle rühma väikseimast suurimasse.
• 2. samm: Rühma paaritu / paarisarvu mediaani leidmise meetod on toodud allpool:
• 3. samm: kui elementide arv rühmas on paaritu - leidke {(n + 1) / 2} termin. Sellele terminile vastav väärtus on mediaan.
• 4. samm: kui rühma elementide arv on ühtlane - leidke selles rühmas {(n + 1) / 2} kolmas termin ja keskpunkt mediaanpositsiooni mõlemal küljel olevate arvude vahel. Näiteks kui on 8 vaatlust, on mediaan (8 + 1) / 2. positsioon, mis on 4.5. Mediaan, saab arvutada, lisades selle rühma 4. ja 5. termini, mis jagatakse seejärel 2-ga.

Keskmise valemi näited statistikas

Selle Median Formula Exceli malli saate alla laadida siit - Median Formula Exceli mall

Näide 1

Arvude loetelu: 4, 10, 7, 15, 2. Arvutage mediaan.

Lahendus: korraldame numbrid kasvavas järjekorras.

Kasvavas järjekorras on numbrid: 2,4,7,10,15

Numbreid on kokku 5. Mediaan on (n + 1) / 2. Väärtus. Seega on mediaan (5 + 1) / 2. väärtus.

Mediaan = 3. väärtus.

Loendis 2, 4, 7 , 10, 15 on 3. väärtus 7.

Seega on mediaan 7.

Näide 2

Oletame, et organisatsioonis on 10 töötajat, sealhulgas tegevjuht. Tegevdirektor Adam Smith on seisukohal, et töötajate poolt tõmmatud palk on kõrge. Ta soovib mõõta rühma väljatöötatud palka ja seega otsuseid langetada.

Allpool on mainitud ettevõtte töötajatele antud töötasu. Arvutage mediaanpalk. Palgad on $ 5000, $ 6000, $ 4000, $ 7,000, $ 8,000, $ 7500, $ 10,000, $ 12,000, $ 4500, $ 10,00,000

Lahendus:

Korraldame palgad kõigepealt kasvavas järjekorras. Palgad kasvavas järjekorras on:

4000, 4500, 5000, 6000, 7000, 7500, 8000, 10 000, 12 000, 10 000 000 dollarit

Seetõttu arvutatakse mediaan järgmiselt:

Kuna on 10 üksust, on mediaan (10 + 1) / 2. Mediaan = 5,5 punkt.

Seega on mediaan 5. ja 6. üksuse keskmine. 5. ja 6. üksus on 7000 dollarit ja 7500 dollarit.

= (7000 dollarit + 7500 dollarit) / 2 = 7250 dollarit.

Seega on 10 töötaja keskmine palk = 7250 dollarit.

Näide # 3

Tootmisorganisatsiooni tegevjuht Jeff Smith peab asendama 7 masinat uute vastu. Ta on mures tekkivate kulude pärast ja kutsub seetõttu ettevõtte finantsjuhti, et aidata tal arvutada seitsme uue masina mediaanmaksumus.

Finantsjuht soovitas uusi masinaid osta ainult siis, kui masinate mediaanhind on alla 85 000 dollari. Kulud on järgmised: 75 000, 82 500, 60 000, 50 000, 1 000 000, 70 000, 90 000 USD. Arvutage masinate keskmine maksumus. Kulud on järgmised: 75 000, 82 500, 60 000, 50 000, 1 000 000, 70 000, 90 000 USD.

Lahendus: 

Kulude järjestamine kasvavas järjekorras: 50 000, 60 000, 70 000, 75 000, 82 500, 90 000, 1 000 000 dollarit.

Seetõttu arvutatakse mediaan järgmiselt:

Kuna üksusi on 7, on mediaan (7 + 1) / 2. element ehk 4. element. 4. element on 75 000 dollarit.

Kuna mediaan on alla 85 000 dollari, saab uusi masinaid osta.

Asjakohasus ja kasutusalad

Mediaani peamine eelis keskmise suhtes on see, et äärmuslikud väärtused, mis on väga suured ja väga madalad, ei mõjuta seda põhjendamatult. Seega annab see indiviidile parema ettekujutuse esinduslikust väärtusest. Näiteks kui 5 inimese kaal kilogrammides on 50, 55, 55, 60 ja 150. Keskmine on (50 + 55 + 55 + 60 + 150) / 5 = 74 kg. Kuid 74 kg ei ole tõeline tüüpiline väärtus, kuna suurem osa kaaludest jääb vahemikku 50–60. Arvutame sellisel juhul mediaani. See oleks (5 + 1) / 2. ametiaeg = 3. ametiaeg. Kolmas tähtaeg on 55 kg, mis on mediaan. Kuna suurem osa andmetest jääb vahemikku 50–60, on 55 kg andmete tõeline representatiivne väärtus.

Mediaani tähenduse tõlgendamisel peame olema ettevaatlikud. Näiteks kui me ütleme, et keskmine kaal on 55 kg, ei kehti kõik 55 kg. Mõni võib kaaluda rohkem, mõni kaaluda vähem. 55 kg on aga hea näitaja 5 inimese kehakaalule.

Reaalses maailmas võib keskmise suuruse või väikese väärtuse arv moonutada selliste andmekogumite mõistmist nagu leibkonna sissetulek või leibkonna vara, mis on väga erinevad. Seega kasutatakse mediaani, et soovitada, mis peaks olema tüüpiline väärtus.

Keskmine valem statistikas (Exceli malliga)

Bill on kingapoe omanik. Ta tahab teada, millise suurusega kingi ta peaks tellima. Ta küsib 9 kliendilt, mis suurusega on nende kingad. Tulemused on 7, 6, 8, 8, 10, 6, 7, 9, 6. Arvutage mediaan, et aidata Billi tema tellimisotsuses.

Lahendus: kõigepealt peame korraldama kingade suurused kasvavas järjekorras.

Need on: 6, 6, 6, 7, 7, 8, 8, 9, 10

Allpool on toodud kingapoe mediaani arvutamise andmed.

Seetõttu arvutatakse mediaan excelis järgmiselt,

Excelis on mediaani jaoks sisseehitatud valem, mida saab kasutada arvude rühma mediaani arvutamiseks. Valige tühi lahter ja tippige see = MEDIAN (B2: B10) (B2: B10 tähistab vahemikku, mille mediaani soovite arvutada).

Kingapoe mediaan on -