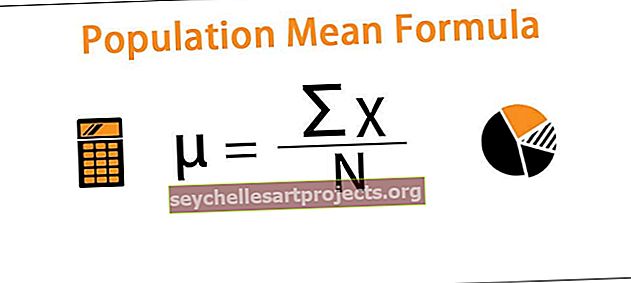seychellesartprojects.org

Valim proovivea arvutamiseks

Valimivigade valem viitab valemile, mida kasutatakse statistilise vea arvutamiseks, mis tekib olukorras, kus testi läbiviija ei vali valimit, mis esindaks kogu vaadeldavat populatsiooni, ja valemi järgi arvutatakse valimiviga jagades populatsiooni standardhälve valimi suuruse ruutjuurega ja korrutatakse saadud tulemus Z-skoori väärtusega, mis põhineb usaldusvahemikul.

Prooviviga = Z x (σ / √ n)

Kus

• Z on usaldusvahemiku põhjal Z-skoori väärtus
• σ on populatsiooni standardhälve
• n on valimi suurus

Proovivea arvutamine samm-sammult

• 1. samm : koguti kogu populatsiooniks nimetatud andmekogum. Arvutage populatsiooni keskmine ja populatsiooni standardhälve.
• 2. samm : Nüüd tuleb kindlaks määrata valimi suurus ja lisaks peab valimi suurus olema väiksem kui populatsioon ja see ei tohiks olla suurem.
• 3. samm : määrake kindlaks usaldustase ja vastavalt sellele saab selle tabelist määrata Z-skoori väärtuse.
• 4. samm : korrutage Z skoor populatsiooni standardhälbega ja jagage see valimi suuruse ruutjuurega, et saada vea piir või valimi suuruse viga.

Näited

Selle proovivõtuvea valemi Exceli malli saate alla laadida siit - valimi vigade valemi Exceli mall

Näide 1

Oletame, et populatsiooni standardhälve on 0,30 ja valimi suurus 100. Milline on valimi viga 95% usaldusväärsuse tasemel?

Lahendus

Siin antakse meile nii populatsiooni standardhälve kui ka valimi suurus, seetõttu võime sama arvutamiseks kasutada järgmist valemit.

Kasutage arvutamiseks järgmisi andmeid.

Seetõttu on valimi vea arvutamine järgmine,

Valimi viga on -

Näide 2

Gautam jätkab praegu raamatupidamise kursust ja ta on oma sisseastumiseksami ära teinud. Ta on nüüd registreerunud keskastmele ja liitub praktikandina ka vanemraamatupidajaga. Ta töötab tootmisettevõtete auditis. 

Ühel firmal, keda ta esimest korda külastas, paluti kontrollida, kas kõigi ostutööde arved on mõistlikult saadaval. Tema valitud valimi suurus oli 50 ja sama populatsiooni standardhälve oli 0,50.

Olemasoleva teabe põhjal peate arvutama valimi vea 95% ja 99% usaldusvahemiku korral.

Lahendus

Siin antakse meile nii populatsiooni standardhälve kui ka valimi suurus, seetõttu võime sama arvutamiseks kasutada järgmist valemit.

Z-skoor 95% -lise usaldustaseme korral on 1,96 (saadaval Z-i tabelist)

Kasutage arvutamiseks järgmisi andmeid.

Seetõttu on arvutus järgmine,

Valimi viga on -

95-protsendilise usaldustaseme Z-skoor on 2,58 (saadaval Z-skoori tabelist)

Kasutage arvutamiseks järgmisi andmeid.

Seetõttu on arvutus järgmine,

Valimi viga on -

Usaldustaseme suurenedes suureneb ka valimiviga.

Näide # 3

Koolis korraldati biomeetriline seanss, et kontrollida õpilaste tervist. Seanss algatati X klassi standardi õpilastega. Kokku on B-divisjonis 30 õpilast. Nende hulgas valiti juhuslikult 12 õpilast, kes tegid üksikasjalikku ülevaatust ja puhkasid. Tehti ainus põhitesti. Aruandest järeldati, et B-divisjoni õpilaste keskmine pikkus on 154.

Lahendus

Populatsiooni standardhälve oli 9,39. Ülaltoodud teabe põhjal peate arvutama valimisvea 90% ja 95% usaldusvahemiku jaoks.

Siin antakse meile nii populatsiooni standardhälve kui ka valimi suurus, seetõttu võime sama arvutamiseks kasutada järgmist valemit.

Z-skoor 95% -lise usaldustaseme korral on 1,96 (saadaval Z-i tabelist)

Kasutage arvutamiseks järgmisi andmeid.

Seetõttu on valimi vea arvutamine järgmine,

Valimi viga on -

Z-skoor 90% -se usaldustaseme korral on 1,645 (saadaval Z-i tabelist)

Kasutage arvutamiseks järgmisi andmeid.

Seetõttu on arvutus järgmine,

Valimi viga on -

Usaldustaseme langedes väheneb ka valimiviga.

Asjakohasus ja kasutusalad

Selle kontseptsiooni mõistmiseks on see väga oluline, kuna see näitab, kui palju võib eeldada, et uuringu tulemused kujutaksid tegelikult kogu elanikkonna tegelikku vaadet. Tuleb meeles pidada ühte asja, et uuringu läbiviimiseks kasutatakse väiksemat populatsiooni, mida nimetatakse valimi suuruseks (mida muidu nimetatakse ka uuringu vastajateks), et esindada suuremat elanikkonda.

Seda võib vaadelda kui uuringu tõhususe arvutamise viisi. Kui valimimarginaal on suurem, näitab see, et uuringu tagajärjed võivad kalduda kõrvale tegelikust kogu rahvastiku esindatusest. Teisest küljest on valimiviga või vea piir väiksem kui see, mis näitab, et tagajärjed on nüüd lähemal kogu populatsiooni tegelikule esindatusele ja mis loob vaadeldava uuringu suhtes suurema usalduse.