Edasimäära valem | Definitsioon ja arvutamine (koos näidetega)
Valem tuleviku määra arvutamiseks
Tuleviku intressimäärade valem aitab lahti mõtestada tulukõverat, mis on graafiline esitus erinevate võlakirjade tootlustest, millel on erinevad tähtajad. Seda saab arvutada lähima tuleviku kuupäeva ja lähema tuleviku kuupäeva ning järgmise tuleviku ja lähema tuleviku kuupäevani kulunud aastate arvu põhjal.
Edasisuunamise määr = [(1 + S 1 ) n 1 / (1 + S 2 ) n 2 ] 1 / (n 1 -n 2 ) - 1kus S 1 = spot-kurss kuni järgmise tuleviku kuupäevani,
- S 2 = spot-intress kuni lähema tuleviku kuupäevani, n 1 = aastate arv järgmise järgmise kuupäevani,
- n 2 = aastate arv lähema tuleviku kuupäevani
Valemi tähistust tähistatakse tavaliselt kui F (2,1), mis tähendab ühe aasta määra kahe aasta pärast.
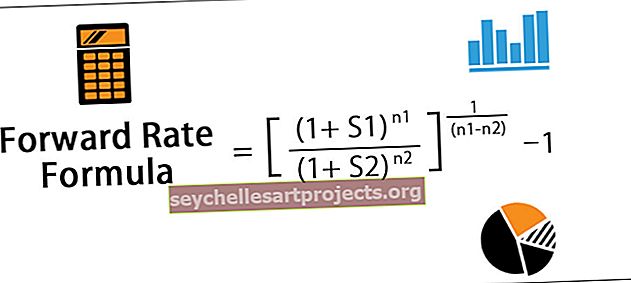
Edasimäära arvutamine (samm-sammult)
Selle saab tuletada järgmiste sammude abil:
- 1. samm: esiteks määrake väärtpaberi ostu või müügi tulevase kuupäevani spot-intressimäär ja seda tähistatakse tähisega S 1 . Samuti arvutage nr. aasta kuni järgmise tuleviku kuupäevani ja seda tähistatakse n 1-ga .
- 2. samm: Seejärel määrake sama väärtpaberi müümise või ostmise lähim tuleviku kuupäev hetkemäär ja seda tähistatakse tähisega S 2 . Seejärel arvutage nr. aasta lähima tuleviku kuupäevani ja seda tähistatakse n 2-ga .
- Samm 3: Lõpuks arvutatakse tuleviku intressimäär (n 1 - n 2 ) nr. aastate pärast n 2 ei. aastate kohta on näidatud allpool. Forward rate = [(1 + S 1 ) n 1 / (1 + S 2 ) n 2 ] 1 / (n 1 -n 2 ) - 1
Näited
Selle Edastamise määra valemi Exceli malli saate alla laadida siit - Edastamise määra valemi Exceli mallNäide 1
Võtame näiteks ettevõtte PQR Ltd, kes on hiljuti emiteerinud võlakirju, et koguda raha oma järgmise kahe aasta jooksul valmiva projekti jaoks. Üheaastase tähtajaga emiteeritud võlakirjad on pakkunud investeeringutasuvuseks 6,5%, kaheaastase tähtajaga võlakirjad investeeringutasuvuseks 7,5%. Arvestage antud andmete põhjal ühe aasta määr ühe aasta pärast.
Arvestades
- Kahe aasta spot-intressimäär, S 1 = 7,5%
- Aasta spot-intressimäär, S 2 = 6,5%
- 2. võlakirja aastaarv, n 1 = 2 aastat
- 1. võlakirjade aastate arv, n 2 = 1 aasta

Vastavalt ülaltoodud andmetele arvutame nüüd ettevõtte POR ltd ühe aasta intressimäära.
Seetõttu arvutatakse ühe aasta forward-intressimäär ühe aasta pärast,

F (1,1) = [(1 + S 1 ) n 1 / (1 + S 2 ) n 2 ] 1 / (n 1- n 2 ) -
= [(1 + 7,5%) 2 / (1 + 6,5%) 1] 1 / (2-1) - 1

Üks aasta FR ühe aasta pärast = 8,51%
Näide 2
Võtame näiteks maaklerfirma, mis on selles valdkonnas tegutsenud üle kümne aasta. Firma on esitanud järgmise teabe. Tabelis on toodud ülevaade tuleviku intressimäära üksikasjalikust arvutamisest.
- Spot-intressimäär üheks aastaks, S 1 = 5,00%
- F (1,1) = 6,50%
- F (1,2) = 6,00%
Arvestage antud andmete põhjal kahe ja kolme aasta spot-intressimäär. Seejärel arvutage ühe aasta forward-intressimäär kahe aasta pärast.
- Arvestades, S 1 = 5,00%
- F (1,1) = 6,50%
- F (1,2) = 6,00%

Seetõttu saab kahe aasta hetkemäära arvutada järgmiselt:
S 2 = [(1 + S 1 ) * (1 + F (1,1))] 1/2 - 1
= [(1 + 5,00%) * (1 + 6,50%)] 1/2 -

Spot-määr kahe aasta jooksul = 5,75%
Seetõttu on spot-intressimäära arvutamine kolmeks aastaks
S 3 = [(1 + S 1 ) * (1 + F (1,2)) 2] 1/3 -
= [(1 + 5,00%) * (1 + 6,00%) 2] 1/3 -

Spot-määr kolmeks aastaks = 5,67%
Seetõttu arvutatakse ühe aasta forward-intressimäär kahe aasta pärast,

F (2,1) = [(1 + S 3 ) 3 / (1 + S 2 ) 2] 1 / (3-2) -
= [(1 + 5,67%) 3 / (1 + 5,75%) 2] -

Asjakohasus ja kasutusalad
Forvardkurss viitab kursile, mida kasutatakse makse diskonteerimiseks kaugemast tuleviku kuupäevast lähemale tulevikule. Seda võib vaadelda ka kahe tulevase spot-intressi, st edasise spot-intressi ja lähema spot-intressimäära, vahelise seosena. See on hinnang selle kohta, millised on turu hinnangul tulevikus erineva tähtajaga intressimäärad.
Oletagem näiteks, et Jack on täna raha saanud ja ta soovib ühe aasta jooksul kinnisvara ostmiseks raha kokku hoida. Nüüd saab ta raha investeerida valitsuse väärtpaberitesse, et see oleks järgmiseks aastaks ohutu ja likviidne. Sellisel juhul on Jackil kaks valikut: ta saab kas osta riigivõlakirja, mille tähtaeg lõpeb ühe aasta jooksul, või ta võib osta teise riigivõlakirja, mis saab tähtajaks kuue kuu pärast, ja seejärel üle viia raha veel kuue kuu pärast -kuune riigivõlakiri, kui esimene lõpeb.
Juhul, kui mõlemad võimalused toovad sama investeeringutasuvuse, on Jack ükskõikne ja jätkab mõlemat võimalust. Aga mis siis, kui pakutav intress on kuuekuulise võlakirja eest kõrgem kui üheaastane võlakiri. Sellisel juhul teenib ta rohkem raha, ostes praegu kuue kuu võlakirja ja viies selle veel kuueks kuuks üle. Nüüd tuleb mängu kuue kuu võlakirja tootluse arvutamine kuue kuu pärast. Sel moel võib see aidata Jackil sellist ajapõhist saagikuse muutust ära kasutada.