Populatsiooni dispersiooni valem | Samm-sammult arvutamine | Näited
Valem populatsiooni dispersiooni arvutamiseks
Populatsiooni dispersioonivalem on rahvastikuandmete keskmiste kauguste mõõt ja see arvutatakse populatsiooni valemi keskmise välja selgitamise teel ja dispersioon arvutatakse muutujate ruudu summa, millest lahutatakse keskmine, mis jagatakse arvukate vaatluste arvuga populatsioonis.
Rahvastiku varieeruvus on rahvastikuandmete leviku mõõt. Seega võib populatsiooni varieeruvust määratleda kui keskmist vahemaad igast konkreetse populatsiooni andmepunktist keskmiseni, ruutu ja see näitab, kuidas andmepunktid on populatsioonis hajutatud. Populatsiooni varieeruvus on statistikas kasutatav oluline hajuvuse mõõt. Statistikud arvutavad dispersiooni, et teha kindlaks, kuidas andmekogumi üksikud numbrid omavahel suhestuvad.
Populatsiooni dispersiooni arvutamisel arvutatakse hajuvus populatsiooni keskmise põhjal. Seega peame populatsiooni varieeruvuse arvutamiseks välja selgitama populatsiooni keskmise. Üks populaarsemaid teateid populatsiooni dispersiooni kohta on σ2. Seda hääldatakse sigma ruuduna.
Populatsiooni dispersiooni saab arvutada järgmise valemi abil:


kus
- σ2 on populatsiooni dispersioon,
- x 1, x 2 , x 3, ... ..x n on vaatlused
- N on vaatluste arv,
- µ on andmekogumi keskmine
Rahvastiku dispersiooni arvutamine samm-sammult
Populatsiooni dispersiooni valemit saab arvutada järgmise viie lihtsa toimingu abil:
- 1. samm: arvutage antud andmete keskmine (µ). Keskmise arvutamiseks lisage kõik vaatlused ja jagage see vaatluste arvuga (N).
- 2. samm: tehke tabel. Pange tähele, et tabeli koostamine ei ole kohustuslik, kuid selle tabelina esitamine muudaks arvutused lihtsamaks. Kirjutage esimesse veergu kõik vaatlused (x 1, x 2 , x 3, ... ..x n ).
- 3. samm: kirjutage teise veergu iga vaatluse hälve keskmisest (x i - µ).
- 4. samm: kirjutage kolmandasse veergu iga vaatluse ruut keskmise (x i - µ) 2 põhjal. Teisisõnu ruudutage iga veerus 2 saadud arv.
- 5. samm: Seejärel peame lisama kolmandas veerus saadud arvud. Leidke ruutude hälvete summa ja jagage saadud summa vaatluste arvuga (N). See aitab meil saada
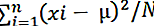 populatsiooni dispersiooni.
populatsiooni dispersiooni.
Näited
Selle Population Variance Formula Exceli malli saate alla laadida siit - Population Variance Formula Exceli mallNäide 1
Arvutage populatsiooni dispersioon järgmise 5 vaatluse põhjal: 50, 55, 45, 60, 40.
Lahendus:
Populatsiooni dispersiooni arvutamiseks kasutage järgmisi andmeid.

Kokku on 5 vaatlust. Seega N = 5.
µ = (50 + 55 + 45 + 60 + 40) / 5 = 250/5 = 50
Seega saab populatsiooni dispersiooni σ2 arvutada järgmiselt.


σ2 = 250/5
Populatsiooni dispersioon σ2 saab olema

Populatsiooni dispersioon (σ2) = 50
Populatsiooni dispersioon on 50.
Näide 2
XYZ Ltd. on väikeettevõte ja koosneb ainult 6 töötajast. Tegevjuht usub, et nende töötajate palkades ei tohiks olla suurt hajuvust. Sel eesmärgil soovib ta, et arvutaksite nende palkade dispersiooni. Nende töötajate palgad on nagu alla. Arvutage tegevjuhi palkade rahvastiku varieeruvus.
Lahendus:
Populatsiooni dispersiooni arvutamiseks kasutage järgmisi andmeid.

Kokku on 6 vaatlust. Seega N = 6.
= (30 + 27 + 20 + 40 + 32 + 31) / 6 = 180/6 = 30 dollarit
Seega saab populatsiooni dispersiooni σ2 arvutada järgmiselt.


σ2 = 214/6
Populatsiooni dispersioon σ2 saab olema

Rahvaarvu dispersioon (σ2) = 35,67
Elanikkonna palga varieeruvus on 35,67.
Näide # 3
Sweet Juice Ltd toodab erinevaid maitset. Juhtimisosakond ostab selle mahla tehases ladustamiseks 7 suurt mahutit. Kvaliteedikontrolli osakond otsustas, et lükkab konteinerid tagasi, kui konteinerite dispersioon on suurem kui 10. Arvestades 7 konteineri kaalu kilogrammides: 105, 100, 102, 95, 100, 98 ja 107. Palun andke kvaliteedile teada Kontrolliosakond selle kohta, kas ta peaks konteinerid tagasi lükkama.
Lahendus:
Populatsiooni dispersiooni arvutamiseks kasutage järgmisi andmeid.

Vaatlusi on kokku 7. Seega N = 7
= (105 + 100 + 102 + 95 + 100 + 98 + 107) / 7 = 707/7 = 10
Seega saab populatsiooni dispersiooni σ2 arvutada järgmiselt.


σ2 = 100/7
Populatsiooni dispersioon σ2 saab olema

Rahvaarvu dispersioon (σ2) = 14,29
Kuna dispersioon (14.29) ületab kvaliteedikontrolli osakonna määratud 10 piiri, tuleks konteinerid tagasi lükata.
Näide 4
Sagar Healthcare nimelise haigla juhtkond registreeris, et 2019. aasta märtsi esimesel nädalal oli sündinud 8 last. Arst soovis hinnata nii imikute tervist kui ka kõrguste dispersiooni. Nende beebide kõrgused on järgmised: 48 cm, 47 cm, 50 cm, 53 cm, 50 cm, 52 cm, 51 cm, 60 cm. Arvutage nende 8 beebi kõrguste dispersioon.
Lahendus:
Populatsiooni dispersiooni arvutamiseks kasutage järgmisi andmeid.

Seega saab populatsiooni dispersiooni σ2 arvutada järgmiselt.

Excelis on populatsiooni dispersiooni sisseehitatud valem, mida saab kasutada arvude rühma populatsiooni dispersiooni arvutamiseks. Valige tühi lahter ja tippige see valem = VAR.P (B2: B9). Siin on B2: B9 lahtrite vahemik, mille põhjal soovite arvutada populatsiooni dispersiooni.
Populatsiooni dispersioon σ2 saab olema

Rahvaarvu dispersioon (σ2) = 13,98
Asjakohasus ja kasutamine
Hajumise mõõduna kasutatakse populatsiooni variatsiooni. Vaatleme kahte populatsiooni komplekti, millel on sama keskmine ja vaatluste arv. Andmekomplekt 1 koosneb 5 numbrist - 55, 50, 45, 50 ja 50. Andmekogum 2 koosneb 10, 50, 85, 90 ja 15. Mõlemal andmekogumil on sama keskmine, mis on 50. Kuid andmekogumis 1 on väärtused üksteise lähedal, samas kui andmekogumil 2 on väärtused hajutatud. Dispersioon annab selle läheduse / hajutatuse teadusliku mõõtmise. Andmekogumi 1 dispersioon on ainult 10, andmekogumil 2 on tohutu dispersioon 1130. Seega näitab suur dispersioon, et arvud on keskmisest kaugel ja üksteisest kaugel. Väike dispersioon näitab, et numbrid on üksteise lähedal.
Variatsioonide haldamisel kasutatakse varieerumist varieerumisel. Investorid arvutavad optimaalsete portfellide kindlaksmääramiseks varade tootluse dispersiooni, optimeerides kahte peamist parameetrit - tootlust ja volatiilsust. Dispersiooniga mõõdetud volatiilsus on konkreetse rahalise tagatise riski mõõt.

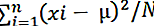 populatsiooni dispersiooni.
populatsiooni dispersiooni.