Portfelli dispersioonivalem (näide) | Kuidas arvutada portfelli dispersiooni?
Mis on portfelli dispersioon?
Mõiste „portfelli variatsioon“ viitab tänapäevase investeerimisteooria statistilisele väärtusele, mis aitab mõõta portfelli keskmise tootluse hajumist selle keskmisest. Lühidalt, see määrab portfelli kogu riski. Selle saab tuletada individuaalse dispersiooni ja vastastikuse kovariantsuse kaalutud keskmise põhjal.
Portfelli varieeruvuse valem
Matemaatiliselt esitatakse kahest varast koosnev portfellidispersioonivalem järgmiselt:
Portfelli dispersioonivalem = w 1 2 * ơ 1 2 + w 2 2 * ơ 2 2 + 2 * ρ 1,2 * w 1 * w 2 * ơ 1 * ơ 2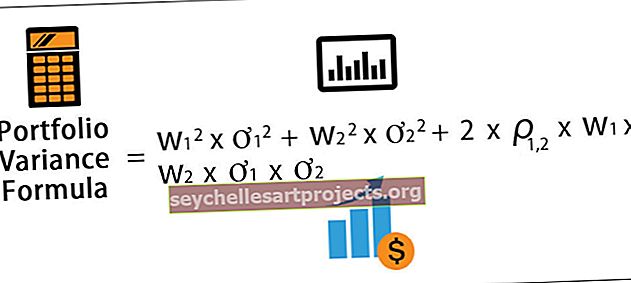
kus
- w i = vara i portfelli kaal
- ơ i 2 = vara i individuaalne varieeruvus
- ρ i, j = korrelatsioon i ja vara j vahel
Jällegi saab dispersiooni veelgi laiendada portfellile, kus on rohkem nr. näiteks kolme varaga portfelli võib kujutada näiteks
Portfelli dispersioonivalem = w 1 2 * ơ 1 2 + w 2 2 * ơ 2 2 + w 3 2 * ơ 3 2 + 2 * ρ 1,2 * w 1 * w 2 * ơ 1 * ơ 2 + 2 * ρ 2,3 * w 2 * w 3 * ơ 2 * ơ 3 + 2 * ρ 3,1 * w 3 * w 1 * ơ 3* ơ 1
Portfelli variatsioonivalemi selgitus
Konkreetse portfelli varieeruvuse valemi saab tuletada järgmiste sammude abil:
1. samm: kõigepealt määrake iga vara kaal kogu portfellis ja see arvutatakse, jagades vara väärtuse portfelli koguväärtusega. I-nda vara kaalu tähistatakse w i-ga .
2. samm: Seejärel määrake iga vara standardhälve ja see arvutatakse iga vara keskmise ja tegeliku tootluse põhjal. I-nda vara standardhälvet tähistatakse tähisega ơ i . Standardhälbe ruut on dispersioon, st ơ i 2.
3. samm: Seejärel määrake varade vaheline korrelatsioon ja see kajastab põhimõtteliselt iga vara liikumist teise vara suhtes. Korrelatsiooni tähistatakse ρ-ga.
4. samm: lõpuks tuletatakse kahe vara portfellidispersioonivalem individuaalse dispersiooni ja vastastikuse kovariantsuse kaalutud keskmise põhjal, nagu allpool näidatud.
Portfelli dispersioonivalem = w 1 * ơ 1 2 + w 2 * ơ 2 2 + 2 * ρ 1,2 * w 1 * w 2 * ơ 1 * ơ 2
Näide portfelli varieeruvuse valemist (koos Exceli malliga)
Selle portfelli variatsiooni valemi Exceli malli saate alla laadida siit - portfelli variatsiooni valemi Exceli mall
Võtame näiteks portfelli, mis koosneb kahest aktsiast. Aktsia A väärtus on 60 000 dollarit ja selle standardhälve on 15%, aktsia B väärtus aga 90 000 dollarit ja standardhälve 10%. Kahe aktsia vahel on korrelatsioon 0,85. Määrake dispersioon.
Arvestades
- Varu A standardhälve, ơ A = 15%
- Varu B standardhälve, ơ B = 10%
Korrelatsioon, ρ A, B = 0,85
Allpool on esitatud andmed kahe aktsia portfelli varieeruvuse arvutamiseks.

Aktsia kaal, w A = 60 000 dollarit / (60 000 dollarit + 90 000 dollarit) * 100%

Aktsia kaal = 40% või 0,40
B aktsia kaal, w B = 90 000 dollarit / (60 000 dollarit + 90 000 dollarit) * 100%

B-aktsia kaal = 60% või 0,60
Seetõttu on portfelli dispersiooni arvutamine järgmine,

Dispersioon = w A 2 * ơ A 2 + w B 2 * ơ B 2 + 2 * ρ A, B * w A * w B * ơ A * ơ B
= 0,4 ^ 2 * (0,15) 2 + 0,6 ^ 2 * (0,10) 2 + 2 * 0,85 * 0,4 * 0,6 * 0,15 * 0,10

Seetõttu on dispersioon 1,33%.
Asjakohasus ja kasutamine
Portfellivarude üks silmatorkavamaid omadusi on asjaolu, et selle väärtus tuletatakse iga varade individuaalsete dispersioonide kaalutud keskmise põhjal, mida on korrigeeritud nende kovariatsioonidega. See näitab, et üldine dispersioon on väiksem kui portfelli iga aktsia üksikute variatsioonide kaalutud keskmine. Tuleb märkida, et väiksema korrelatsiooniga väärtpaberitega portfelli portfelli varieeruvus on väiksem.
Portfellide dispersioonivalemi mõistmine on samuti oluline, kuna see leiab rakenduse moodsas portfelliteoorias, mis põhineb eeldusel, et tavalised investorid kavatsevad oma tootlust maksimeerida, minimeerides samas riski, näiteks dispersiooni. Investor jälgib tavaliselt seda, mida nimetatakse tõhusaks piiriks, ja see on madalaim riski või volatiilsuse tase, mille juures investor võib saavutada oma eesmärgi tasuvuse. Kõige sagedamini investeerivad investorid riski vähendamiseks korreleerimata varadesse vastavalt kaasaegsele portfelliteooriale.
On juhtumeid, kus varad, mis võivad olla üksikult riskantsed, võivad lõpuks vähendada portfelli varieeruvust, sest selline investeering tõenäoliselt suureneb teiste investeeringute langedes. Sellisena võib selline vähenenud korrelatsioon aidata hüpoteetilise portfelli varieeruvust vähendada. Tavaliselt hinnatakse portfelli riskitaset standardhälbe abil, mis arvutatakse dispersiooni ruutjuurena. Eeldatakse, et dispersioon püsib suur, kui andmepunktid on keskmisest kaugel, mille tulemuseks on ka portfelli üldine suurem riskitase.