seychellesartprojects.org

F-testi valemi määratlus

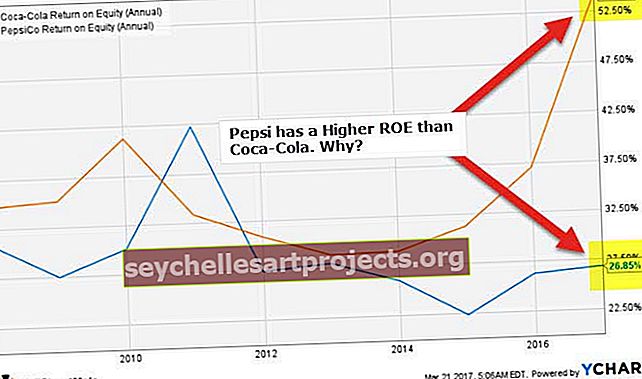
F-testi valemit kasutatakse statistilise testi tegemiseks, mis aitab testi läbiviijal tuvastada, kas kahel populatsioonikogumil, millel on nende andmepunktide normaalne jaotus, on sama standardhälve või mitte.

F-Test on mis tahes test, mis kasutab F-jaotust. F väärtus on väärtus F jaotuses. Erinevad statistilised testid genereerivad F-väärtuse. Väärtuse abil saab kindlaks teha, kas test on statistiliselt oluline. Kahe dispersiooni võrdlemiseks tuleb arvutada kahe dispersiooni suhe, mis on järgmine:

F väärtus = suurem valimi dispersioon / väiksem valimi dispersioon = σ ₁ 2 / σ ₂ 2

Kuigi F-test Excelis, peame raamistama null- ja alternatiivhüpoteesid. Seejärel peame kindlaks määrama testi olulisuse taseme. Järgnevalt peame välja selgitama nii lugeja kui nimetaja vabadusastmed. See aitab määrata tabeli F väärtust. Seejärel võrreldakse tabelis nähtavat F-väärtust arvutatud F-väärtusega, et teha kindlaks, kas nullhüpotees lükatakse tagasi.

F-testi arvutamine samm-sammult

Allpool on toodud etapid, kus F-Testi valemit kasutatakse hüpoteesi nullimiseks, et kahe populatsiooni variatsioonid on võrdsed:

• 1. samm: esiteks koostage null- ja alternatiivhüpotees. Nullhüpotees eeldab, et dispersioonid on võrdsed. H ₀ : σ ₁ 2 = σ ₂ 2 . Alternatiivhüpotees väidab, et dispersioonid on ebavõrdsed. H ₁ : σ ₁ 2 _≠  σ ₂ 2 . Siin on σ ₁ 2 ja σ ₂ 2 dispersioonide sümbolid.
• 2. samm: arvutage teststatistika (F jaotus). st = σ ₁ 2 / σ ₂ 2, kus eeldatakse, et σ ₁ 2 on suurem valimi dispersioon ja σ ₂ 2 on väiksem valimi dispersioon
• 3. samm: arvutage vabadusastmed. Vabadusaste (df ₁ ) = n ₁ - 1 ja vabaduse aste (df ₂ ) = n ₂ - 1, kus n ₁ ja n ₂ on valimi suurused
• 4. samm:   vaadake tabelis F väärtust F. Kahe sabaga testi korral jagage alfa kahega, et leida õige kriitiline väärtus. Seega leitakse F väärtus lugedes lugeja vabadusastmeid ja tabelis F nimetajat. Df ₁ loetakse ülemisest reast läbi. Esimene veerg loetakse ette Df ₂ .

Märkus. Erineva tähtsusastmega on olemas erinevad F-tabelid. Ülal on F-tabel alfa = .050 jaoks.

• 5. samm: võrrelge 2. etapis saadud F-statistikat 4. etapis saadud kriitilise väärtusega. Kui F-statistika on vajalikul olulisuse tasemel suurem kui kriitiline väärtus, lükkame nullhüpoteesi tagasi. Kui 2. etapis saadud F-statistika on nõutaval olulisuse tasemel väiksem kui kriitiline väärtus, ei saa me nullhüpoteesi tagasi lükata.

Näited

Selle F Test Formula Exceli malli saate alla laadida siit - F Test Formula Exceli mall

Näide 1

Statistikat tegi F-testi. Ta sai F-statistikaks 2.38. Tema saadud vabadusastmed olid 8 ja 3. Uurige F-tabelist välja F-väärtus ja tehke kindlaks, kas suudame nullhüpoteesi tagasi lükata 5-protsendise olulisuse juures (ühe sabaga test).

Lahendus:

F tabelist peame otsima 8 ja 3 vabadusastet. Tabelist saadud F kriitiline väärtus on 8,845 . Kuna F statistika (2.38) on väiksem kui F tabeli väärtus (8.845), ei saa me nullhüpoteesi tagasi lükata.

Näide 2

Kindlustusselts müüb tervisekindlustust ja liikluskindlustuse poliise. Kliendid maksavad kindlustusmakseid nende poliiside eest. Kindlustusseltsi tegevdirektor küsib, kas mõlema kindlustussegmendi (tervisekindlustus ja liikluskindlustus) makstavad kindlustusmaksed on võrreldes teisega erinevamad. Ta leiab makstud preemiate kohta järgmised andmed:

Tehke kahesabaline F-test olulisuse tasemega 10%.

Lahendus:

• 1. samm: tühine hüpotees H ₀ : σ ₁ 2 = σ ₂ 2

Alternatiivne hüpotees H _a : σ ₁ 2 _≠  σ ₂ 2

• 2. etapp: F statistika = F väärtus = σ ₁ 2 / σ ₂ 2 = 200/50 = 4
• Etapp 3: df ₁ = n ₁ - 1 = 11-1 = 10

df _{2 =}  n ₂ - n 1 = 51-1 = 50

• 4. samm: kuna tegemist on kahe sabaga testiga, on alfatase = 0,10 / 2 = 0,050. F-tabeli F-väärtus vabadusastmetega 10 ja 50 on 2,026.
• 5. samm: kuna F statistika (4) on suurem kui saadud tabeli väärtus (2.026), lükkame nullhüpoteesi tagasi.

Näide # 3

Pangal on peakontor Delhis ja filiaal Mumbais. Ühes kontoris on pikad kliendijärjekorrad, teises kontoris on kliendijärjekorrad lühikesed. Panga operatsioonijuht mõtleb, kas ühe filiaali kliendid on muutlikumad kui teise filiaali klientide arv. Ta viib läbi klientide uuringu.

Delhi peakontori klientide dispersioon on 31 ja Mumbai harukontoril 20. Delhi peakontori valimi suurus on 11 ja Mumbai filiaali valim 21. Tehke kahe sabaga F-test olulisuse tasemega 10%.

Lahendus:

• 1. samm:   tühine hüpotees H ₀ : σ ₁ 2 = σ ₂ 2

Alternatiivne hüpotees H _a : σ ₁ 2 _≠  σ ₂ 2

• 2. etapp: F statistika = F väärtus = σ ₁ 2 / σ ₂ 2 = 31/20 = 1,55
• Etapp 3: df ₁ = n ₁ - 1 = 11-1 = 10

df _{2 =}  n ₂ - n 1 = 21-1 = 20

• 4. samm: kuna tegemist on kahe sabaga testiga, on alfatase = 0,10 / 2 = 0,05. F tabeli F väärtus vabadusastmetega 10 ja 20 on 2,348.
• 5. samm: kuna F-statistika (1,55) on väiksem kui saadud tabeli väärtus (2,348), ei saa me nullhüpoteesi tagasi lükata.

Asjakohasus ja kasutusalad

F-Testi valemit saab kasutada väga erinevates seadetes. F-testi kasutatakse hüpoteesi kontrollimiseks, et kahe populatsiooni dispersioonid on võrdsed. Teiseks kasutatakse seda hüpoteesi kontrollimiseks, et normaalse jaotusega ja sama standardhälbega populatsioonide keskmised on võrdsed. Kolmandaks kasutatakse seda hüpoteesi kontrollimiseks, et pakutud regressioonimudel sobib andmetega hästi.

F-testi valem Excelis (Exceli malliga)

Organisatsiooni töötajatele makstakse päevapalka. Organisatsiooni tegevjuht on mures organisatsiooni meeste ja naiste palga erinevuse pärast. Allpool on andmed võetud meeste ja naiste valimist.

Tehke ühe sabaga F-test 5% -lise olulisuse tasemega.

Lahendus:

• 1. samm: H ₀ : σ ₁ 2 = σ ₂ 2, H ₁ : σ ₁ 2 _≠  σ ₂ 2
• 2. samm: klõpsake Exceli vahekaarti Andmed> Andmete analüüs.

• 3. samm: ilmub allpool nimetatud aken. Valige dispersioonide jaoks F-Test Two-Sample ja klõpsake siis nuppu OK.

• 4. samm: klõpsake kasti Muutuja 1 vahemik ja valige vahemik A2: A8. Klõpsake kasti Muutuja 2 vahemik ja valige vahemik B2: B7. Klõpsake väljundivahemikus A10. Valige alfaks 0,05, kuna olulisuse tase on 5%. Seejärel klõpsake nuppu OK.

F statistika ja tabeli F väärtused kuvatakse koos muude andmetega.

• 4. samm: ülaltoodud tabelist näeme, et F statistika (8.296) on suurem kui F kriitiline ühe saba (4.95), seega lükkame nullhüpoteesi tagasi.

Märkus 1: Muutuja 1 dispersioon peab olema suurem kui muutuja 2 dispersioon. Vastasel juhul on Exceli tehtud arvutused valed. Kui ei, siis vahetage andmed.

Märkus 2: Kui Andmete analüüsi nupp pole Excelis saadaval, avage Fail> Valikud. Valige pistikprogrammide alt Analysis ToolPak ja klõpsake nuppu Mine. Kontrollige Analysis Tool Packi ja klõpsake nuppu OK.

Märkus 3: Exceli tabelis F on arvutatud valem. Selle süntaks on: