seychellesartprojects.org

Efektiivse intressimäära määratlus

Efektiivne intressimäär, mida nimetatakse ka aasta ekvivalendimääraks, on intressimäär, mida inimene tegelikult maksab või teenib finantsinstrumendi eest ja mis arvutatakse, arvestades liitmise mõju ajavahemikul.

Efektiivne intressimäära valem

Efektiivse intressimäära valem = (1 + i / n) n -

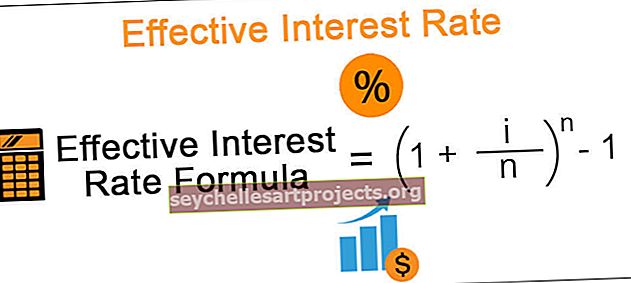
Siin i = instrumendis mainitud aastane intressimäär.

n = See tähistab liitperioodide arvu aastas.

Tõlgendused

Liitmine muudab intressimäära. Sellepärast ei ole instrumendile kirjutatud intressimäär investorile efektiivne intressimäär (aastane ekvivalentmäär). Näiteks kui instrumendile kirjutatakse 11% intressimäär ja intressimäära suurendatakse neli korda aastas, ei saa aastane ekvivalentmäär olla 11%.

Mis see siis oleks?

See oleks - (1 + i / n) n - 1 = (1 + 0,11 / 4) 4 - 1 = 1,1123 - 1 = 0,1112 = 11,23%.

See tähendab, et investori tegelik intressimäär oleks 11,23%.

Isegi kui muutus on väike, ei ole see sama kui instrumendis nimetatud aasta intressimäär.

Näide

Näide 1

Ting ostis konkreetse pilli. Instrumendi mainitud intressimäär on 16%. Ta on investeerinud umbes 100 000 dollarit. Instrument ühendub igal aastal. Milline oleks selle konkreetse instrumendi tegelik intressimäär (AER)? Kui palju ta saaks igal aastal huvi?

Efektiivne intressimäär ja aastane intressimäär ei ole alati ühesugused, sest intressid suurenevad igal aastal mitu korda. Mõnikord suureneb intressimäär poolaastas, kvartalis või kuus. Ja nii erineb aastane ekvivalentmäär aasta intressimäärast.

See näide näitab teile seda.

Arvutame välja.

Kuna intressimäär liitub igal aastal, on siin efektiivse intressimäära valem -

(1 + i / n) n - 1 = (1 + 0,16 / 1) 1 - 1 = 1,16 - 1 = 0,16 = 16%.

See tähendab, et selles konkreetses näites ei oleks aasta intressimäära ja aastase ekvivalentmäära (AER) vahel vahet.

Igal aastal saab Ting instrumendi intressi = (100 000 dollarit * 16%) = 16 000 dollarit.

Näide 2

Tong ostis konkreetse pilli. Instrumendi mainitud intressimäär on 16%. Ta on investeerinud umbes 100 000 dollarit. Pill ühendatakse kuus korda aastas. Kui suur oleks selle konkreetse instrumendi aastane ekvivalentmäär (AER)? Kui palju ta saaks igal aastal huvi?

See on vaid eelmise näite pikendus.

Kuid seal on tohutu erinevus.

Eelmises näites lisati instrument üks kord aastas, mis muutis aasta intressimäära sarnaseks aastase samaväärse määraga.

Kuid sel juhul on stsenaarium täiesti erinev.

Siin on intressimäär, mis liitub kuus korda aastas.

Nii, siin on aasta intressimäära valem -

(1 + i / n) n - 1 = (1 + 0,16 / 6) 6 - 1 = 1,171 - 1 = 0,171 = 17,1%.

Nüüd näete, et kui intressimäära suurendatakse kuus korda aastas, muutub aastane ekvivalentmäär hoopis erinevaks.

Nüüd, kui meil on efektiivne intressimäär, saame arvutada intressi, mida Tong saab aasta lõpus.

Tong saab = (100 000 dollarit * 17,1%) = 17 100 dollarit.

Kui võrrelda intressi, mille Ting sai eelmises näites, Tongi intressiga, kui intressimäärad muutuvad erinevalt, näeme, et intresside erinevus on umbes 1100 dollarit.

Näide 3

Ping on investeerinud instrumenti. Ta on investeerinud 10 000 dollarit. Instrumendis nimetatud intressimäär on 18%. Intress liitub igakuiselt. Uurige, kuidas esimesel aastal saab Ping iga kuu intressi.

See on palju üksikasjalikum näide aasta ekvivalendimäärast.

Selles näites näitame, kuidas arvutamine tegelikult toimub ilma efektiivse intressimäära valemit kasutamata.

Vaatame järele.

Kuna intressimäär liitub igakuiselt, on nimetatud intressimäära tegelik jagunemine kuus = (18/12) = 1,5%.

• Esimesel kuul saab Ping intressi = (10 000 * 1,5%) = 150 dollarit.
• Teisel kuul saab Ping intressi = {(10 000 + 150) * 1,5%} = (10 150 * 1,5%) = 152,25 dollarit.
• Kolmandal kuul saab Ping intressi = {(10 000 + 150 + 152,25) * 1,5%} = (10 302,25 * 1,5%) = 154,53 dollarit.
• Neljandal kuul saab Ping intressi = {(10 000 + 150 + 152,25 + 154,53) * 1,5%} = (10 456,78 * 1,5%) = 156,85 dollarit.
• Viiendal kuul saab Ping intressi = {(10 000 + 150 + 152,25 + 154,53 + 156,85) * 1,5%} = (10 613,63 * 1,5%) = 159,20 dollarit.
• Kuuendal kuul saab Ping intressi = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20) * 1,5%} = (10 772,83 * 1,5%) = 161,59 dollarit.
• Seitsmendal kuul saab Ping intressi = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59) * 1,5%} = (10 934,42 * 1,5%) = 164,02 dollarit.
• Kaheksandal kuul saab Ping intressi = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02) * 1,5%} = (11098,44 * 1,5%) = 166,48 dollarit.
• Üheksandal kuul saab Ping intressi = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48) * 1,5%} = (11264,92 * 1,5%) = 168,97 dollarit.
• Kümnendal kuul saab Ping intressi = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48 + 168,97) * 1,5%} = (11433,89 * 1,5%) = 171,51 dollarit.
• Üheteistkümnendal kuul saab Ping intressi = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48 + 168,97 + 171,51) * 1,5%} = (11605,40 * 1,5%) = 174,09 dollarit.
• Kaheteistkümnendal kuul saab Ping intressi = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48 + 168,97 + 171,51 + 174,09) * 1,5%} = (11779,49 * 1,5%) = 176,69 dollarit.

Pingi kogu aasta huvi kokku on -

• (150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48 + 168,97 + 171,51 + 174,09 + 176,69) = 1956,18 dollarit.

• Aastane ekvivalentsimäära valem = (1 + i / n) n - 1 = (1 + 0,18 / 12) 12 - 1 = 1,195618 - 1 = 0,195188 = 19,5618%.

Niisiis, intress, mille Ping saaks = ($ 10 000 ^ 19,5618%) = $ 1956,18.

Efektiivne intressimäär Excelis

Efektiivse intressimäära või aastase ekvivalentmäära leidmiseks excelis kasutame Exceli funktsiooni EFFECT.

• nominaalne_hind on intressimäär
• nper on liitumisperioodide arv aastas

Vaatame allpool toodud näidet

• Kui teie nominaalne intressimäär on 10% aastas, on aastane ekvivalentmäär sama, mis 10%.
• Kui teie nominaalne intressimäär on 10% liitmisena kuue kuu jooksul, on aastane ekvivalentmäär sama, mis 10,25%.
• Kui teil on kvartali nominaalne intressimäär 10%, on aastane ekvivalentmäär sama, mis 10,38%.
• Kui teie nominaalne intressimäär on 10% kuus, on aastane ekvivalentmäär sama, mis 10,47%.
• Kui teie nominaalintressimäär on 10% päevas, on tegelik intressimäär sama, mis 10,52%.

Soovitatavad lugemised

See oli efektiivse intressimäära ja selle määratluse juhend. Siin käsitleme efektiivse intressimäära valemit koos sammhaaval arvutustega. Lisateavet leiate järgmistest artiklitest

• Negatiivse intressimäära näide
• Arvutage osavõtumäär
• Erinevused - diskontomäär vs intressimäär
• Nominaalne intressimäära valem
• Koostamine
<