P väärtuse valem | Näited samm-sammult P-väärtuse arvutamiseks
Mis on P-väärtuse valem?
P on statistiline meede, mis aitab teadlastel kindlaks teha, kas nende hüpotees on õige. See aitab kindlaks teha tulemuste olulisuse. Nullhüpotees on vaikepositsioon, et kahe mõõdetud nähtuse vahel puudub seos. Seda tähistatakse H 0. Alternatiivne hüpotees on see, mida võiksite arvata, kui nullhüpotees osutuks valetuks. Selle sümbol on H 1 või H a.
Exceli P-väärtus on arv vahemikus 0 kuni 1. P-väärtuse arvutamiseks on abiks tabelid, arvutustabeliprogrammid ja statistiline tarkvara. Olulisuse tase (α) on uurija poolt eelnevalt kindlaksmääratud künnis. See on üldiselt 0,05. Väga väike p-väärtus, mis on väiksem kui olulisuse tase, näitab, et lükkate nullhüpoteesi tagasi. P-väärtus, mis on olulisuse tasemest suurem, näitab, et nullhüpoteesi ei lükata tagasi.
P-väärtuse valemi selgitus
Valemi p-väärtuse arvutamiseks saab tuletada järgmiste sammude abil:
P-väärtuse arvutamine Z-statistika põhjal
1. samm: peame välja selgitama testistatistika z

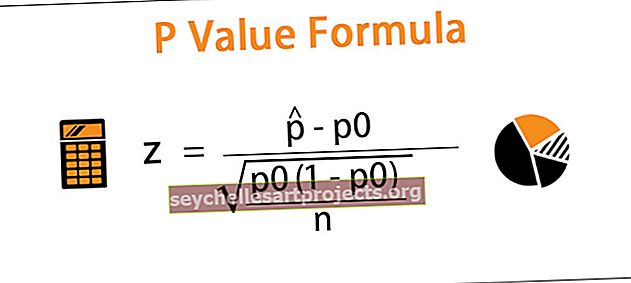
Kus
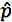 on proovi proportsioon
on proovi proportsioon- p0 on oletatav populatsiooni osakaal nullhüpoteesis
- n on valimi suurus
2. samm: saadud z väärtusest peame leidma vastava p-taseme. Sel eesmärgil peame vaatama tabelit z.

Allikas: www.dummies.com
Näiteks leiame p väärtus, mis vastab z ≥ 2,81. Kuna normaaljaotus on sümmeetriline, on z negatiivsed väärtused võrdsed selle positiivsete väärtustega. 2,81 on summa 2,80 ja 0,01. Vaadake veerus z 2,8 ja vastavat väärtust 0,01. Saame p = 0,0025.
P-väärtuse valemi näited (koos Exceli malliga)
Vaatame P-väärtuse võrrandi lihtsamaid ja täpsemaid näiteid, et sellest paremini aru saada.
Selle P Value Formula Exceli malli saate alla laadida siit - P Value Formula Exceli mall
Näide 1
a) P-väärtus on 0,3015. Kui olulisuse tase on 5%, leidke nullhüpotees tagasi.
b) P-väärtus on 0,0129. Kui olulisuse tase on 5%, leidke nullhüpotees tagasi.
Lahendus:
P-väärtuse arvutamiseks kasutage järgmisi andmeid.

P-väärtus on -

a) Kuna p-väärtus 0,3015 on suurem kui olulisuse tase 0,05 (5%), ei saa me nullhüpoteesi tagasi lükata.
b) Kuna p-väärtus 0,01129 on väiksem kui olulisuse tase 0,05, lükkame nullhüpoteesi tagasi.
Näide 2
Uuringu kohaselt räägib 27% India inimestest hindi keelt. Uurija on uudishimulik, kas see näitaja on tema külas kõrgem. Seega loob ta null- ja alternatiivhüpoteesi. Ta testib H 0: p = 0,27. Ha : p> 0,27. Siin on p hindi keelt kõnelevate inimeste osakaal külas. Ta tellib oma külas uuringu, et selgitada välja hindi keelt oskavate inimeste arv. Ta leiab, et valimisse kuuluvast 240 inimesest 80 oskab hindi keelt. Uurige uurija testi ligikaudne p-väärtus, kui peaksime eeldama, et vajalikud tingimused on täidetud ja olulisuse tase on 5%.
Lahendus:
P-väärtuse arvutamiseks kasutage järgmisi andmeid.

Siin on valimi suurus n = 240,
p 0 on populatsiooni osakaal Peame leidma valimi osakaalu
= 80/240
 = 0,33
= 0,33
Z Statistika
Z statistika arvutamine


= 0,33 - 0,27 / √ 0,27 * (1 - 0,27) / 240
Z Statistika on -

Z = 2,093696
P väärtus on -

P väärtus = P (z ≥ 2,09)
Peame vaatama, et väärtus 2.09 on tabel z. Niisiis, me peame vaatama veerus -2,0 ja veerus 0,09 olevat väärtust. Kuna normaaljaotus on sümmeetriline, on kõverast paremal asuv ala võrdne vasakpoolsega. Saame p-väärtuseks 0,0183.
P väärtus = 0,0183
Kuna p-väärtus on väiksem kui oluline tase 0,05 (5%), lükkame nullhüpoteesi tagasi.
Märkus . Excelis on p-väärtus tulemuseks 0,0181
Näide # 3
Uuringud näitavad, et mehed ostavad rohkem lennupileteid kui naised. Neid ostavad mehed ja naised vahekorras 2: 1. Uuring viidi läbi konkreetses India lennujaamas, et leida lennupiletite jaotus meestele ja naistele. 150 piletist ostsid 88 piletit isased ja 62 piletit. Peame välja selgitama, kas eksperimentaalne manipuleerimine põhjustab muutusi tulemustes või jälgime juhuse variatsiooni. Arvutage p-väärtus, eeldades, et olulisuse aste on 0,05.
Lahendus:
P-väärtuse arvutamiseks kasutage järgmisi andmeid.

1. samm: täheldatud väärtus on meestel 88 ja naistel 62.
- Eeldatav väärtus meestel = 2/3 * 150 = 100 meest
- Eeldatav väärtus emastele = 1/3 * 150 = 50 emast
2. samm: saate teada chi-ruudu


= ((88-100) 2) / 100 + (62-50) 2/50
= 1,44 + 2,88
Chi-ruut (X ^ 2)
Chi-ruut (X ^ 2) saab olema -

Chi-ruut (X ^ 2) = 4,32
3. samm: leidke vabadusastmed
Kuna muutujaid on 2 - mehed ja naised, n = 2
Vabadusastmed = n-1 = 2-1 =
4. samm: p-väärtuste tabelist vaatame tabeli esimest rida, kuna vabadusaste on 1. Näeme, et p-väärtus on vahemikus 0,025–0,05. Kuna p-väärtus on väiksem kui olulisuse aste 0,05, lükkame nullhüpoteesi tagasi.
P-väärtus on -

P väärtus = 0,037666922
Märkus. Excel annab p-väärtuse otse valemi abil:
CHITEST (tegelik vahemik, eeldatav vahemik)
Näide 4
On teada, et 60% linnas rõivakauplustesse sisenevatest inimestest ostab midagi. Rõivakaupluse omanik soovis teada saada, kas tema omanduses oleva rõivakaupluse arv on suurem. Tal olid juba oma poe jaoks läbi viidud uuringu tulemused. Tema poodi sisenenud 200 inimesest 128 ostsid midagi. Poeomanik tähistas passi nende inimeste osakaalu, kes sisenesid tema rõivapoodi ja ostsid midagi. Tema koostatud nullhüpotees oli p = 0,60 ja alternatiivne hüpotees p> 0,60. Leidke uuringu p-väärtus olulisuse tasemel 5%.
Lahendus:
P-väärtuse arvutamiseks kasutage järgmisi andmeid.

Siin valimi suurus n = 200. Peame leidma valimi proportsiooni
= 128/200
 = 0,64
= 0,64
Z Statistika
Z statistika arvutamine


= 0,64 - 0,60 / √ 0,60 * (1 - 0,60) / 200
Z Statistika on -

Z Statistika = 1,1547
P väärtus = P (z ≥ 1,1547)
Funktsioon NORMSDIST Excelis

NORMSDIST on -

NORMSDIST = 0,875893461
Excelis asuva statistika põhjal p-väärtuse arvutamiseks on sisseehitatud funktsioon. Seda tuntakse kui funktsiooni NORMSDIST. Funktsioon Exceli NORMSDIST arvutab standardväärtuse normaalse kumulatiivse jaotuse funktsiooni. Selle formaat on NORMSDIST (z). Kuna z statistiline väärtus on lahtris B2, on kasutatav funktsioon = NORMSDIST (B2).
P väärtus on -

P väärtus = 0,12410654
Kuna peame leidma kõverast paremal asuva ala,
p-väärtus = 1 - 0,875893 = 0,1224107
Kuna p-väärtus 0,1224107 on suurem kui oluline tase 0,05, ei saa me nullhüpoteesi tagasi lükata.
Asjakohasus ja kasutamine
P-väärtusel on statistiliste hüpoteeside testimisel palju rakendusi, täpsemalt nullhüpoteeside testimisel. Näiteks juhib fondihaldur investeerimisfondi. Ta väidab, et investeerimisfondi konkreetse skeemi tootlus on võrdne Niftyga, mis on aktsiaturu võrdlusindeks. Ta raamistaks nullhüpoteesi, et investeerimisfondide skeemi tootlus on samaväärne Nifty tootlusega. Alternatiivne hüpotees oleks, et skeemi tulud ja Nifty tootlused ei ole samaväärsed. Seejärel arvutas ta p-väärtuse.

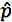 on proovi proportsioon
on proovi proportsioon