seychellesartprojects.org

Z-testi arvutamise valem statistikas

Z Test statistikas viitab hüpoteesitestile, mida kasutatakse selleks, et teha kindlaks, kas kaks arvutatud valimi keskmist on erinevad, juhul kui standardhälbed on olemas ja valim on suur.

   Z = (x - μ) / ơ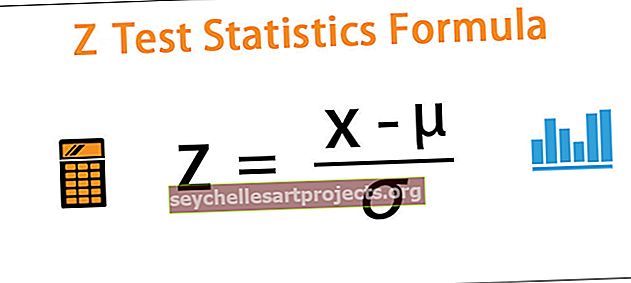      

kus x = mis tahes väärtus populatsioonist

• μ = populatsiooni keskmine
• population = populatsiooni standardhälve

Valimi korral arvutatakse väärtuse z-testi statistika valem, lahutades x-väärtusest valimi keskmise ja seejärel jagatakse tulemus valimi standardhälbega. Matemaatiliselt on see esindatud järgmiselt:

Z = (x - x_mean ) / s

kus

• x = valimi mis tahes väärtus
• x_mean = valimi keskmine
• s = proovi standardhälve

Z Testarvutus (samm-sammult)

Populatsiooni z-testi statistika valem tuletatakse järgmiste sammude abil:

• 1. samm: kõigepealt arvutage populatsiooni keskmine ja populatsiooni standardhälve populatsiooni keskmisse jääva vaatluse põhjal ja iga vaatlust tähistatakse tähega x _i . Vaatluste koguarvu populatsioonis tähistab N.

Rahvastiku keskmine,

Populatsiooni standardhälve,

• 2. etapp: Lõpuks arvutatakse z-testi statistika, lahutades muutujast populatsiooni keskmine ja seejärel jagatakse tulemus populatsiooni standardhälbega, nagu allpool näidatud.

Z = (x - μ) / ơ

Valimi z-testi statistika valem tuletatakse järgmiste sammude abil:

• 1. samm: kõigepealt arvutage valimi keskmine ja proovi standardhälve sama, mis ülaltoodud. Siin tähistatakse valimis olevate vaatluste koguarv n-ga, nii et n <N.

Keskmine proov,

Proovi standardhälve,

• 2. etapp: lõpuks arvutatakse z-testi statistika, lahutades x-väärtusest valimi keskmine ja seejärel jagatakse tulemus valimi standardhälbega, nagu allpool näidatud.

Z = (x - x_mean ) / s

Näited

Selle Z Test Formula Exceli malli saate alla laadida siit - Z Test Formula Exceli mall

Näide 1

Oletagem, et koolis on õpilasi, kes ilmusid klassi kontrolltööle. Katse keskmine tulemus on 75 ja standardhälve on 15. Määrake testil 90 punkti saanud Davidi z-testi tulemus.

Arvestades

• Populatsiooni keskmine, μ = 75
• Populatsiooni standardhälve, ơ = 15

Seetõttu saab z-testi statistikat arvutada järgmiselt:

Z = (90 - 75) / 15

Z Teststatistika on -

• Z = 1

Seetõttu on Davidi testi tulemus ühe standardhälbega üle populatsiooni keskmise tulemuse, st vastavalt z-skoori tabelile on 84,13% õpilastest vähem punkte kui David.

Näide 2

Võtame näiteks 30 õpilast, kes valiti küsitletava näidisrühma koosseisu, et näha, mitu pliiatsit nädalas kasutati. Määrake vastuste põhjal 3. õpilase z-testi tulemus: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 , 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7.

Arvestades

• x = 5, kuna 3. õpilase vastus on 5
• Valimi suurus, n = 30

Keskmine valim = (3 + 2 + 5 + 6 + 4 + 7 + 4 + 3 + 3 + 8 + 3 + 1 + 3 + 6 + 5 + 2 + 4 + 3 + 6 + 4 + 5 + 2 + 2 + 4 + 4 + 2 + 8 + 3 + 6 + 7) / 30

Keskmine = 4,17

Nüüd saab proovi standardhälbe arvutada ülaltoodud valemi abil.

ơ = 1,90

Seetõttu saab 3. õpilase z-testi skoori arvutada järgmiselt:

Z = (x - x) / s

• Z = (5–17) / 1,90
• Z = 0,44

Seetõttu on 3. õpilase kasutamine 0,44-kordne standardhälve valimi keskmisest kasutusest suurem, st z-skoori tabeli järgi kasutab 67% õpilastest vähem pliiatseid kui 3. õpilane.

Näide # 3

Võtame näiteks 30 õpilast, kes valiti küsitletava näidisrühma koosseisu, et näha, mitu pliiatsit nädalas kasutati. Määrake vastuste põhjal 3. õpilase z-testi tulemus: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 , 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7.

Allpool on esitatud andmed Z-testi statistika arvutamiseks

Z teststatistika üksikasjaliku arvutamise kohta saate viidata allpool toodud Exceli lehele.

Asjakohasus ja kasutusalad

Z-testi statistika mõistmine on väga oluline, sest seda kasutatakse tavaliselt alati, kui on vaieldav, kas teststatistika järgib normaalset jaotust asjaomase nullhüpoteesi alusel. Siiski tuleb meeles pidada, et z-testi kasutatakse ainult siis, kui valimi suurus on suurem kui 30, vastasel juhul kasutatakse t-testi.