seychellesartprojects.org

Vähimruutude regressioonimeetodi määratlus

Vähimruutude regressioonimeetod on regressioonanalüüsi vorm, mis määrab sõltuva ja sõltumatu muutuja vahelise seose koos lineaarse joonega. Seda joont nimetatakse "kõige paremini sobituvaks jooneks".

Regressioonanalüüs on statistiline meetod, mille abil saab hinnata või ennustada ühe muutuja tundmatuid väärtusi teise muutuja teadaolevate väärtuste põhjal. Muutuja, mida kasutatakse muutuja intressi ennustamiseks, nimetatakse sõltumatuks või selgitavaks muutujaks ja ennustatavat muutujaks sõltuvaks või selgitatud muutujaks.

Vaatleme kahte muutujat x & y. Need joonistatakse graafikule, mille väärtused on x telje y telje väärtustel x. Neid väärtusi tähistavad punktid alloleval graafikul. Läbi punktide tõmmatakse sirgjoon - seda nimetatakse kõige paremini sobivaks jooneks.

Väikseima ruudu regressiooni eesmärk on tagada, et antud väärtuste hulga kaudu tõmmatud joon looks väärtuste vahel kõige lähema seose.

Vähim ruutude regressioonivalem

Vähimruutude meetodi regressioonijoon arvutatakse järgmise valemi abil -

ŷ = a + bx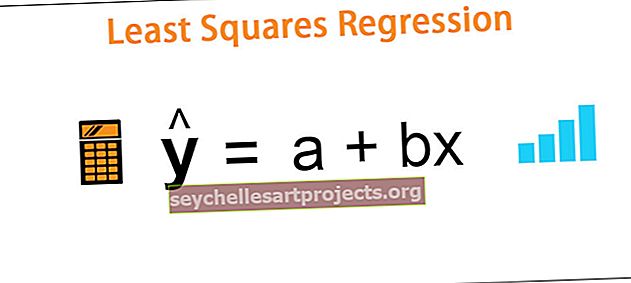

Kus

• dependent = sõltuv muutuja
• x = sõltumatu muutuja
• a = y-lõikepunkt
• b = joone kalle

Joone b kalle arvutatakse järgmise valemi abil -

Või

Y-lõikepunkt arvutatakse "a" järgmise valemi abil -

Parima sobivuse rida väikseima väljaku regressioonis

Parima sobivusega joon on sirge joon, mis on tõmmatud läbi andmepunktide hajumise, mis kõige paremini esindab nende omavahelist suhet.

Vaatleme järgmist graafikut, kus andmehulk on joonistatud piki x- ja y-telge. Neid andmepunkte tähistatakse siniste punktidega. Nende punktide kaudu tõmmatakse kolm joont - roheline, punane ja sinine joon. Roheline joon läbib ühte punkti ja punane joon kolme andmepunkti. Sinine joon läbib aga nelja andmepunkti ning jääkpunktide ja sinise joone vaheline kaugus on kahe teise joonega võrreldes minimaalne.

Ülaltoodud graafikul tähistab sinine joon kõige paremini sobivat joont, kuna see asub kõige lähemal kõikidele väärtustele ning joonest väljaspool olevate punktide ja joone vaheline kaugus on minimaalne (st jääkide ja kõige paremini sobiva joone vaheline kaugus - nimetatud ka jääkide ruutude summadeks). Kahes muus reas, oranžis ja rohelises, on jääkide ja joonte vaheline kaugus sinise joonega võrreldes suurem.

Vähimruutude meetod tagab lähima seose sõltuvate ja sõltumatute muutujate vahel, minimeerides jääkide ja kõige paremini sobiva joone vahelise kauguse, st jääkide ruutude summa on selle lähenemisviisi korral minimaalne. Siit tuleneb mõiste “kõige väiksemad ruudud”.

Vähimruutude regressioonijoone näited

Rakendagem neid valemeid alljärgnevas küsimuses -

Selle kõige vähem ruutude regressiooni Exceli malli saate alla laadida siit - kõige vähem ruutude regressiooni Exceli mall

Näide 1

Üksikasjad, mis käsitlevad tehnikute kogemusi ettevõttes (mitme aasta jooksul) ja nende tööreitingut, on toodud allolevas tabelis. Hinnake neid väärtusi kasutades 20-aastase kogemusega tehniku ​​jõudluse hinnang.

Lahendus -

Väikseimate ruutude arvutamiseks arvutame Y-lõikepunkti (a) ja joone (b) kalle järgmiselt -

Joone (b) kalle

• b = 6727 - [(80 * 648) / 8] / 1018 - [(80) 2/8]
• = 247/218
• = 1,13

Y-lõikepunkt (a)

• a = 648 - (1,13) (80) / 8
• = 69,7

Regressioonijoon arvutatakse järgmiselt -

Asendades valemis x väärtuse 20,

• ŷ = a + bx
• ŷ = 69,7 + (1,13) (20)
• ŷ = 92,3

20-aastase kogemusega tehniku ​​jõudlusreiting on hinnanguliselt 92,3.

Näide 2

Vähim ruutude regressioonivõrrand Exceli abil

Vähimruutude regressioonivõrrandi saab Exceli abil arvutada järgmiste sammudega -

• Andmetabeli lisamine Excelisse.

• Sisestage hajumisgraafik andmepunktide abil.

• Sisestage hajumisgraafikusse trendijoon.

• Trendijoonevalikute alt valige lineaarne trendijoon ja valige diagrammil võrrand.

• Diagrammil kuvatakse antud Exceli andmete kogumi väikseimate ruutude regressioonivõrrand.

Seega arvutatakse antud Exceli andmete kogumi väikseimate ruutude regressioonivõrrand. Võrrandit kasutades võib teha ennustusi ja trendianalüüse. Exceli tööriistad pakuvad ka üksikasjalikke regressiooniarvutusi.

Eelised

• Regressioonanalüüsi vähimruutude meetod sobib kõige paremini ennustusmudelite ja trendianalüüsi jaoks. Seda saab kõige paremini kasutada majanduse, rahanduse ja aktsiaturgude valdkonnas, kus kõigi tulevaste muutujate väärtus ennustatakse olemasolevate muutujate ja nende vaheliste seoste abil.
• Vähimruutude meetod tagab muutujate vahel kõige tihedama seose. Selle meetodi järgi on jääkide ruutude summa kõige paremini sobiva joone vahel minimaalne.
• Arvutusmehhanism on lihtne ja hõlpsasti rakendatav.

Puudused

• Vähimruutude meetod tugineb antud muutujate vahel kõige lähema seose loomisele. Arvutusmehhanism on andmete suhtes tundlik ja kõigi kõrvalekallete (erandlike andmete) korral võivad tulemused enamasti oluliselt mõjutada.
• Seda tüüpi arvutus sobib kõige paremini lineaarsete mudelite jaoks. Mittelineaarsete võrrandite korral rakendatakse ammendavamaid arvutusmehhanisme.

Järeldus

Vähimruutude meetod on üks enim kasutatavaid meetodeid ennustusmudelite ja trendianalüüsi jaoks. Kui see on õigesti arvutatud, annab see parimaid tulemusi.