seychellesartprojects.org

Nõudluse definitsiooni risthindade elastsus

Nõudluse risthindlus mõõdab hinna ja nõudluse vahelist suhet, st ühe toote nõutava koguse muutuse ja teise toote hinna muutuse vahel. Kui mõlemad tooted on asendajad, näitab see nõudluse positiivset rist elastsust ja kui mõlemad on täiendavad kaubad, näitaks see nõudluse kaudset või negatiivset rist elastsust. Lihtsamalt öeldes mõõdab see ühe koguse X nõudluse tundlikkust, kui seotud kauba Y hinda muudetakse.

Nõudluse risthinna elastsuse valem

See arvutatakse, jagades kauba X koguse muutuse protsent kauba Y hinna protsentuaalse muutusega, mis on matemaatiliselt esitatud

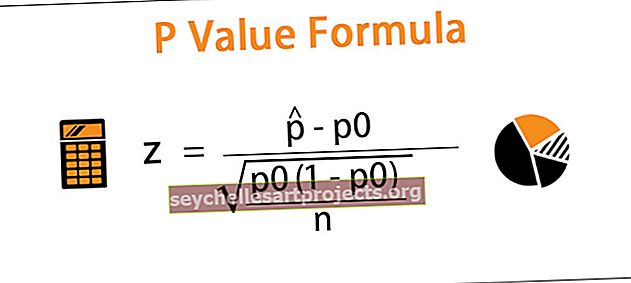
Nõudluse risthinna elastsus = (∆Q _X / Q _X ) ÷ (∆P _Y / P _Y )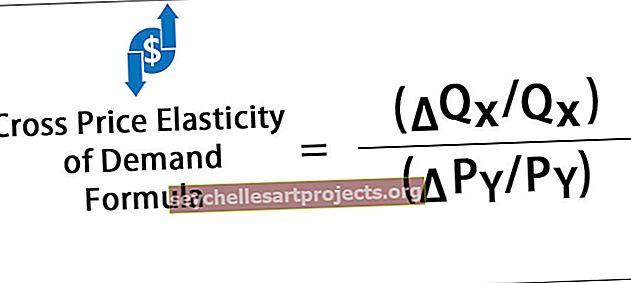

Edasi saab välja töötada nõudluse hinna rist elastsuse valemi

Nõudluse risthinna elastsus = (Q _1X - Q _0X ) / (Q _1X + Q _0X ) ÷ (P _1Y - P _0Y ) / (P _1Y + P _0Y ),

kus

• Q _0X = esialgne nõutav kogus head X-d,
• Q _1X = kauba X lõplik nõutav kogus,
• P _0Y = kauba Y ja alghind
• P _1Y = kauba Y lõplik hind

Nõudluse risthinna elastsuse arvutamine samm-sammult

Seda saab määrata järgmise viie etapiga:

• Samm # 1: Esiteks tuvastage P _0Y ja Q _0X, mis on kauba Y esialgne hind vastavalt algselt nõutud kogus head X-d.
• 2. samm: määrake nüüd kauba X lõplik nõutav kogus ja kauba Y lõplik hind, mida nimetatakse vastavalt Q _1X ja P _1Y .
• Samm # 3: Nüüd töötage välja valemi lugeja, mis tähistab koguse muutust protsentides. Selle saavutamiseks jagatakse lõplike ja algsete suuruste vahe (Q _1X - Q _0X ) lõplike ja algsete suuruste (Q _1X + Q _0X ) summeerimisega, st (Q _1X - Q _0X ) / (Q _1X + Q _0X ).
• 4. samm: töötage välja valemi nimetaja, mis tähistab hinna muutust protsentides. Selle saavutamiseks jagatakse lõplike ja alghindade vahe (P _1Y - P _0Y ) lõplike ja alghindade liitmisega (P _1Y + P _0Y ), st (P _1Y - P _0Y ) / (P _1Y + P _0Y ).
• 5. etapp: lõpuks arvutatakse nõudluse risthindade elastsus, jagades 3. etapi avaldise 4. sammu väljendiga, nagu allpool näidatud.

Nõudluse _risthinna elastsus Valem = (Q _1X - Q _0X ) / (Q _1X + Q _0X ) ÷ (P _1Y - P _0Y ) / (P _1Y + P _0Y )

Näited

Näide 1

Võtame bensiini- ja sõiduautode lihtsa näite. Oletagem nüüd, et bensiini hinna 50% -line tõus põhjustas sõiduautode ostu 10% -list langust. Arvutage antud juhul nõudluse risthindlik elastsus.

Kasutades ülalnimetatud valemit, saab nõudluse risthindade elastsuse arvutada järgmiselt:

Protsendi muutus, siis sõiduautode arv ÷ Protsent muudab bensiini hinda

Kuna võime näha nõudluse rist elastsuse negatiivset väärtust, kinnitab see bensiini- ja sõiduautode täiendavat suhet.

Näide 2

Oletame, et karastusjookide müügiga tegeleb kaks ettevõtet. Praegu müüb ettevõte 2 karastusjooke Y hinnaga 3,50 dollarit pudeli kohta, ettevõte 1 suudab müüa 4000 pudelit karastusjooke Y nädalas. Ettevõtte 1 müügi mõjutamiseks on ettevõte 2 otsustanud langetada hinna 2,50 dollarile, mille tulemusel vähenes 3000 pudelit karastusjooke Y nädalas. Arvutage juhtumi hinna ristnõudlus.

Arvestades, Q _0X = 4000 pudelit, Q _1X = 3000 pudelit, P _0Y = 3,50 dollarit ja P _1Y = 2,50 dollarit

Seetõttu saab nõudluse risthindade elastsuse arvutada ülaltoodud valemi abil,

• Nõudluse risthindlik elastsus = (3000–4000) / (3000 + 4000) ÷ (2,50–3,50 USD) / (2,50–3,50 USD)
• = (-1 / 7) ÷ (-1 / 6)
• = 6/7 või 0,857

Kuna võime näha nõudluse rist elastsuse positiivset väärtust, kinnitab see konkurentsisuhet karastusjoogi X ja karastusjoogi Y vahel.

Asjakohasus ja kasutamine

Ettevõtte jaoks on esmatähtis mõista nõudluse hinnaülese elastsuse mõistet ja asjakohasust, et mõista kauba hinna ja teiselt kaubalt selle hinnaga nõutava koguse suhet. Seda saab kasutada erinevate turgude ning erinevate toodete või teenuste hinnapoliitika otsustamiseks. Risthindade elastsus käitub erinevalt, lähtudes allpool käsitletud kaupade vahelistest suhetest.

# 1 - asendustooted

Juhul kui mõlemad kaubad, mis üksteist täiuslikult asendavad, toovad kaasa täiusliku konkurentsi, toob ühe firmaväärtuse hinnatõus kaasa nõudluse kasvu konkureeriva toote järele. Näiteks erinevad kaubamärgid teravilja on asenduskaupade näited. Tuleb märkida, et kahe asendaja risthindade elastsus on positiivne.

# 2 - täiendavad tooted

Kui üks kaup on täiendav teisele kaubale, siis ühe firmaväärtuse hinna langus toob kaasa täiendava kauba nõudluse kasvu. Mida tugevam on suhe kahe toote vahel, seda suurem on nõudluse hinna rist elastsuse koefitsient. Näiteks mängukonsoolid ja tarkvaramängud on näited täiendavatest kaupadest. Tuleb märkida, et rist elastsus on täiendavate kaupade puhul negatiivne.

# 3 - mitteseotud tooted

Juhul kui kauba vahel pole mingit seost, ei mõjuta ühe kauba hinnatõus teise toote nõudlust. Sellisena on mitteseotud toodetel rist elastsus null. Näiteks taksohindade muutuste mõju turu nõudlusele piima järele.

Video